כל הגופים הסובבים אותנו, החל מכוכבי לכת ועד לחלקיקים הזעירים המרכיבים את האטום, נמצאים במצב של תנועה בלתי-פוסקת. הסוג הפשוט ביותר של תנועה הינו שינוי מיקום של גופים זה ביחס לאחר – תנועה מכנית.

תנועה מכנית הינה הבסיס לפעולת רוב המנגנונים והמכונות, ולתנועה של כל כלי התחבורה הידועים. יחד עם זאת, היא גם מרכיב חשוב בתהליכים שאינם מכניים. כך למשל, תופעות תֶרמִיות קשורות לתנועה מבולגנת של מולקולות; פליטת אור קשורה לתנועתם של אלקטרונים בתוך האטומים; תהליכים גרעיניים – לתנועה ולאינטראקציה של חלקיקים אלמנטריים (פרוטונים, ניטרונים, מזונים). והרשימה ארוכה.

על מנת לתאר תנועה של גוף, יש לציין איך נעות כל הנקודות שלו.
סוג אחד של תנועה של גוף – תנועת העתקה (תנועה טרנסלטורית), בה כל הנקודות של הגוף נעות באופן זהה; ישר המחבר בין שתי נקודות שרירותיות של הגוף, מועתק במקביל לעצמו (איור 1).

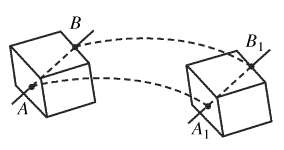
איור מס' 1. תנועת העתקה

ברור כי בכדי לתאר תנועת העתקה של גוף, מספיק לתאר תנועה של נקודה אחת כלשהי שלו.

תנועה סיבובית זהו סוג אחר של תנועה, בה כל הנקודות של הגוף יוצרות מעגלים במישורים מקבילים, כך שמרכזי המעגלים הללו נמצאים על ישר אחד הנקרא ציר הסיבוב (איור 2).

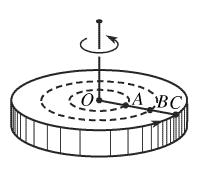
איור מס' 2. תנועה סיבובית

כאשר פותרים בעיות במכניקה, ניתן להתעלם מהמימדים ומהצורה של הגוף בו אנו דנים ולהתייחס אליו כאל מסה נקודתית. מסה נקודתית זהו גוף שניתן להזניח את מימדיו בבעיה הנתונה.
ברור כי מושג המסה הנקודתית הינו מושג מופשט וכי לא קיימות מסות נקודתיות בטבע. אולם בהרבה מקרים, הניסוח של הבעיה מאפשר להשתמש במושג זה ולקבל תוצאות המספיקות למידת הדיוק הנדרשת.
לדוגמה, אם נוסע מעוניין לדעת כמה זמן לוקח למטוס לטוס מתל-אביב לאילת, זה כלל לא חשוב מה אופי התנועה של חלקים שונים של המטוס. יחד עם זאת, כאשר דנים במצבים כמו המראה, נחיתה, התנגדות האוויר וכדומה, לא ניתן להזניח את מימדי המטוס ואת צורתו. באופן דומה, אנו יכולים להתייחס אל כדור הארץ ואל כוכבי לכת אחרים כאל נקודות, אם אנחנו מעוניינים לחקור את אופי תנועתם סביב השמש. אולם אם אנו רוצים לחקור את הסיבה לחילופי עונות השנה או לכך שלילה מתחלף ביום, לא נוכל יותר להתייחס אל כדור הארץ כאל נקודה, ונצטרך לקחת בחשבון את המימדים שלו, את הסיבוב סביב צירו, את השיפוע של ציר הסיבוב ביחס למסלול כדור הארץ וכו’.
לפיכך, במקרים מסוימים אל גוף אחד ניתן להתייחס כאל מסה נקודתית, בעוד שבמקרים אחרים זה לא אפשרי.

מערכת ייחוס ומסלול תנועה

אם נתבונן בתופעות שונות המתרחשות על פני כדור הארץ, ניווכח כי לא כל הכיוונים במרחב שווים; למשל, גוף המשוחרר מהידיים תמיד נע אנכית כלפי מטה (בערך אל מרכז כדור הארץ); בכדי שהגוף ינוע אנכית מעלה יש להקנות לו מהירות התחלתית מסוימת, בעוד שבשביל תנועה אנכית כלפי מטה אין כל צורך במהירות התחלתית. השׁוֹנוּת הזאת של הכיוונים במרחב נובעת מכך שכדור הארץ מושך אליו גופים.
הרחק מכדור הארץ ומשאר כוכבי הלכת, היינו מגלים כי במרחב הריק מגופים גדולים, כל הכיוונים שווים. נהוג לומר כי מרחב ריק הינו איזוטרופ_י, כלומר כל הכיוונים בו זהים ואין בו כיוון מסוים שיש לו תכונה מייחדת כלשהי.
כך גם כל נקודות המרחב הן שוות ערך, אם אין בקרבתן עצמים גדולים מאוד כמו כוכבים או גרמי שמיים אחרים.
_מרחב ריק הינו אחיד (הוֹמוֹגֶנִי), כלומר אין בו נקודות בעלות תכונה מייחדת כלשהי.

גם הזמן הינו אחיד. במילים אחרות, כל המאורעות המתרחשים באותם התנאים אך בזמנים שונים, עוברים באופן זהה לגמרי. אם היום כדור קטן נופל מגובה של 6 מטרים תוך 1,1 שניות, אזי שגם לפני חודש באותה המעבדה לקח לו ליפול מאותו הגובה בדיוק אותו הזמן, ואותו הזמן ייקח לו ליפול באותם התנאים גם אחרי 1000 שנים.

מהעובדה שהמרחב הינו אחיד ואיזוטרופי נובעות כמה מסקנות חשובות ביותר שאציג במאמרים עתידיים. אך ניתן להציג מסקנה אחת חשובה כבר עכשיו: אם המרחב הינו אחיד ואיזוטרופי, הרי שאי אפשר לקבוע מיקום של מסה נקודתית ביחס למרחב.
אולם בהחלט ניתן לקבוע מיקום של גוף כלשהו ביחס לגוף אחר. לדוגמה, ניתן להגדיר מיקום של נורה בחדר באמצעות מרחקה מהרצפה ומשתי הקירות המאונכים זה לזה. באמצעות שלושה מספרים כאלה, ניתן גם לתאר מיקום של כל גוף אחר, בין אם הוא נמצא בתוך החדר או מחוצה לו.
גוף נייח, שביחס אליו קובעים מיקום של כל גוף אחר, נקרא גוף ייחוס.
בדרך כלל מקשרים אל גוף הייחוס שלושה ישרים המאונכים זה לזה הנקראים צירים (איור 3). מיקום של נקודה מבוטא על ידי השיעורים $x, y, z$.

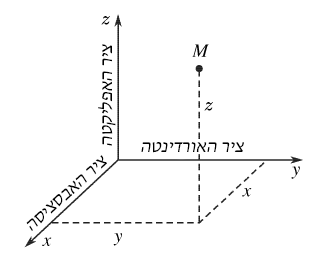
איור מס' 3. מערכת צירים

מערכת ייחוס כוללת שני דברים – מערכת צירים, הקשורה אל גוף ייחוס כלשהו ומכלול שעונים מסונכרנים הממוקמים בנקודות שונות של מערכת הצירים. עקרונית, כל גוף יכול לשמש בתור גוף ייחוס, אולם לא כל מערכות ייחוס עלולות להיות נוחות במידה שווה. למשל, קל יותר לנתח תנועה של מכונית במערכת ייחוס הצמודה אל כדור הארץ, מאשר במערכת ייחוס הצמודה אל השמש או אל הירח. אבל במקרה של כוכבי הלכת, דווקא נוח לעבור למערכת ייחוס הצמודה אל השמש, ולא אל כדור הארץ או אל כוכב לכת אחר – חוקי התנועה של כוכבי הלכת במקרה זה יתוארו בצורה פשוטה יותר.

נקודה הנעה במערכת ייחוס נתונה עוברת בקו הנקרא מסלול. אם נזרוק אבן, אנו נראה כי היא נעה במסלול עקום עד לנפילתה לקרקע. צורת המסלול תלוייה במערכת הייחוס הנבחרת. קל להיווכח שטענה זו נכונה – נניח כי אנו משחררים מהידיים כדור בתוך אוטובוס הנע ביחס לכדור הארץ. ביחס לאוטובוס עצמו, מסלולו של הכדור יהיה קו ישר. אולם ביחס לכדור הארץ, המסלול יהיה עקום (ללא התנגדות האוויר זאת תיהיה פרבולה). דוגמה נוספת היא פּרוֹפֶּלוֹר של מטוס. במערכת ייחוס הצמודה אל מטוס נע, נקודה שרירותית על הפרופלור עוברת מסלול מעגלי (הרי הפרופלור מסתובב); אולם במערכת ייחוס הצמודה אל כדור הארץ, הנקודה עוברת מסלול סלילי.

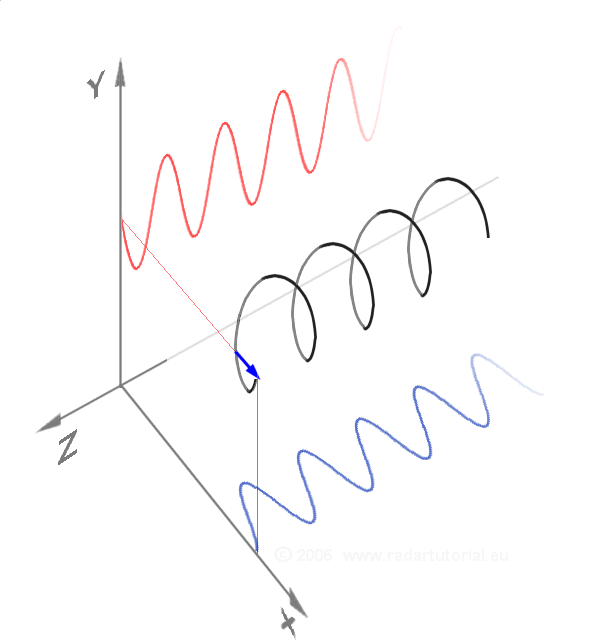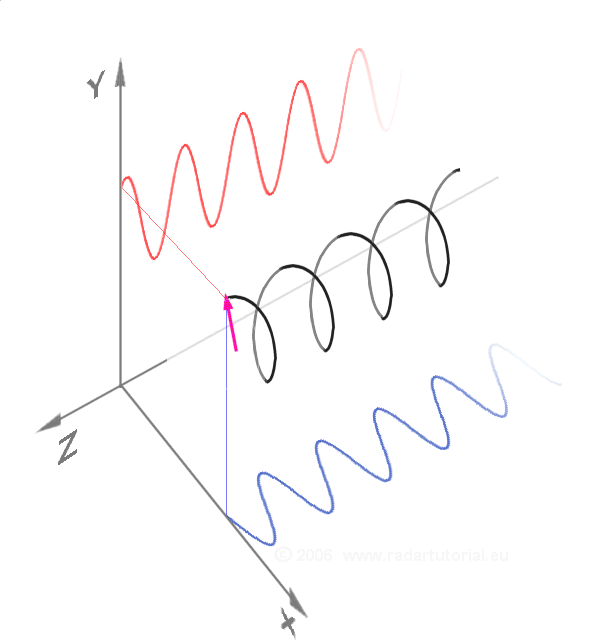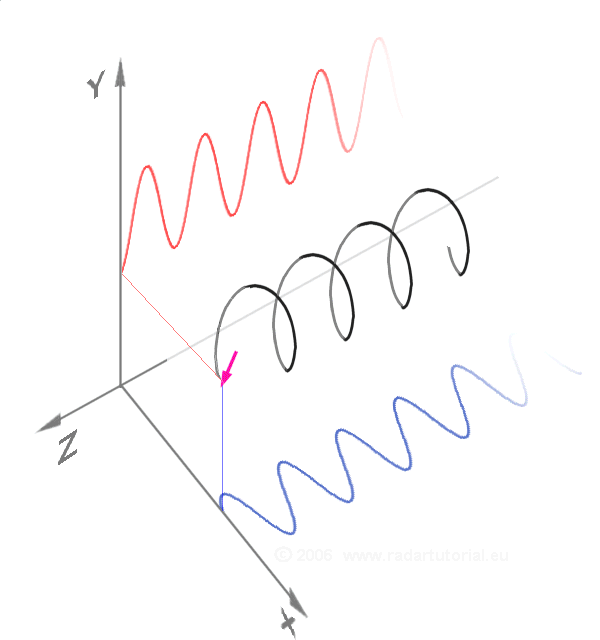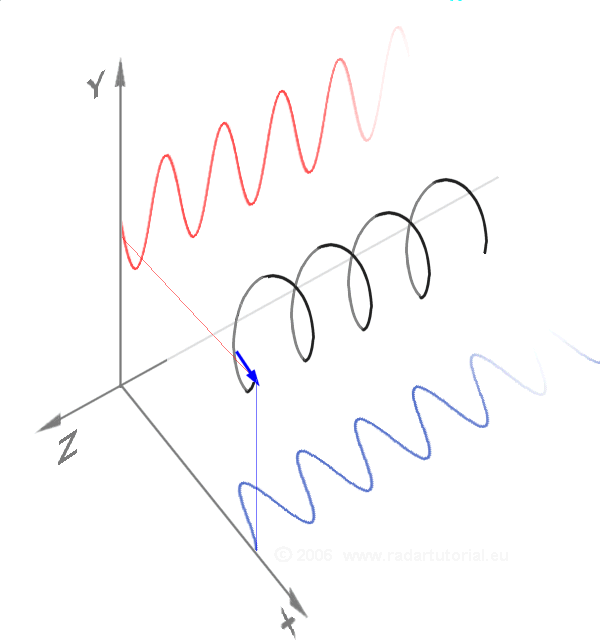
איור 3 – מסלול סלילי (באדיבות ויקימדיה)

לפיכך, מושג צורת המסלול הינו מושג יחסי. לא ניתן לדבר על צורה של מסלול בכלל; אפשר לדבר רק על צורה של מסלול במערכת ייחוס נתונה (מערכת צירים).