תורת היחסות הכללית היא תאוריה מודרנית המקשרת בין כבידה לעקמומיות במרחב-זמן. בגרסתה הקלאסית, שפותחה עוד במאה ה-17 על-ידי אייזק ניוטון, ממשיכים להשתמש גם היום לפתרון בעיות רבות באסטרונומיה, אסטרופיזיקה וקוסמונאוטיקה. ואולם ניוטון בעצמו היה מודע לליקוי בסיסי אחד שהיה קיים במודל שלו – עקרון ה”פעולה מרחוק”. במכניקה ניוטונית, האינטראקציה הכבידתית בין שתי מסות מתרחשת מיד, ללא עיכוב ובלי תלות במרחק בין המסות. וכשם שמקסוול הצליח להיפטר מעקרון הפעולה מרחוק באלקטרודינמיקה (חוק קולון) בעזרת מעבר למשוואות לוקליות כך גם עשה איינשטיין בתורת הגרביטציה.

הסיפור שלנו מתחיל ממאמר שאותו פרסם איינשטיין ב-1905, בו הוא ניסח את תורת היחסות הפרטית ולמעשה השלים מבחינה רעיונית את האלקטרודינמיקה הקלאסית. כמובן שלמאמר קדמו עבודות של לורנץ ופואנקרה אשר כללו אלמנטים רבים של יחסות פרטית. אולם התמונה הכוללת והברורה הופיעה לראשונה רק במאמרו של איינשטיין, וזאת בניגוד לתורת היחסות הכללית, שכל יסודותיה הונחו על ידי איינשטיין. עם זאת, כבר בעבודות של גאוס, רימן, הלמהולץ וקליפורד ניתן לזהות ניצנים של הרעיון הבסיסי לפיו קיים קשר בין הפיזיקה לעיקום המרחב.

גאוס, שחשב על הרעיון של גאומטריה לא-אוקלידית עוד לפני לובצ’בסקי ובויאי (אך לא הספיק לפרסם את המחקר שלו בנושא), גרס כי “אל לו לאיש להציב את הגאומטריה לצד האריתמטיקה – תחום טהור מקדמת דנא – אלא שמוטב להשוותה למכניקה, למשל”. רימן גם הוא התלהב מהרעיון וסבר כי המרחב מעוות (ואף בדיד במרחקים קטנים). מניתוח מידע אסטרונומי הלמהולץ הצליח לקבל מגבלות על עקמומיות המרחב. קליפורד טען כי חומר אינו אלא אדוות במרחב מעוות.

אולם כל הרעיונות הללו הקדימו את זמנם. אי אפשר היה ליצור תורת גרביטציה ללא יחסות פרטית או אלקטרודינמיקה קלאסית, ובלי ההבנה שהמרחב והזמן הם חלק בלתי נפרד מישות אחת – מרחב-זמן (spacetime). הדרך שאיינשטיין נאלץ לעבור כדי לפתח את התאוריה הייתה ארוכה ורוויית מכשולים. לשם השוואה, תורת היחסות הפרטית הוצגה בצורתה הסופית כבר במאמר הראשון (“על האלקטרודינמיקה של גופים נעים”, 1905).

העבודה על תורת הגרביטציה החלה בשנת 1907 ונמשכה מספר שנים. הייתה זאת דרך של ניסוי וטעייה כפי שניתן ללמוד מהמאמרים השונים שאיינשטיין פרסם לאורך אותן השנים. בעיית הכבידה נפתרה באופן סופי בשתי עבודות שהוצגו בפני האקדמיה הפרוסית למדעים בברלין ב-18 ו-25 לנובמבר 1915. בעבודות אלה נוסחו משוואות השדה הגרביטציוני בריק ובנוכחות מקורות כבידה.

בשלבים הסופיים של בניית יחסות כללית השתתף המתמטיקאי הנודע הילברט. בכלל, למתמטיקה (ולמתמטיקאים) חשיבות רבה ביחסות כללית. אנליזה טנזורית – כלי מרכזי ביחסות כללית – פותחה על ידי ריצ’י ולוי-צ’יוויטה. חברו ללימודים של איינשטיין, המתמטיקאי מרסל גרוסמן, היה זה שהכיר לו את הטכניקה של אנליזה טנזורית. ויחד עם זאת, תורת היחסות הכללית היא בראש ובראשונה תורה פיזיקלית, שבבסיסה עקרון פיזיקלי חשוב.

עקרון השקילות וגיאומטריזציה של הכבידה

למעשה, עוד גלילאו גלילאי הבין כי בשדה כבידה (בהיעדר התנגדות אוויר) כל הגופים נעים באותה התאוצה. בדיוק משום כך לא קיימת דרך שתאפשר להבחין בשדה כבידה במעלית הנופלת חופשית. במילים אחרות, במערכת ייחוס הצמודה לגוף שנופל חופשית באזור קטן של מרחב-זמן אין כבידה – זהו אחד הניסוחים של עקרון השקילות.

תכונה זו של שדה כבידה אינה מובנת מאליו. ניזכר למשל בשדה האלקטרומגנטי – קיימים גופים ניטרליים מבחינה חשמלית שכלל לא מושפעים מהשדה. לעומת זאת, בשדה כבידה אין גופים “ניטרליים” – אין שעונים ואין סרגלים שלא מושפעים מגרביטציה. לפיכך, בשדה כבידה הגאומטריה של המרחב הופכת ללא-אוקלידית.

על מנת לקבל איזשהו מושג לגבי מרחבים לא-אוקלידיים נפנה לדוגמה הכי פשוטה של ספירה. ספציפית, נתבונן במשולש כדורי על ספירה – זוהי צורה גאומטרית התחומה על ידי קשתות של מעגלים גדולים (מעגלים שעוברים דרך מרכז הספירה) שחוצים זה את זה, כפי שמתואר באיור הבא:

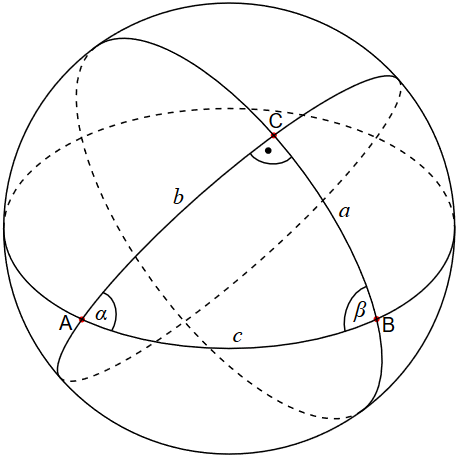
איור 1 – משולש כדורי (באדיבות ויקימדיה)

כאן הקשתות $a$, $b$ ו-$c$ תוחמות משולש כדורי $ABC$. נשים לב כי כל קשת כזאת היא בעצם המסלול הקצר ביותר בין נקודות הקצה שלה, בדומה לקו ישר שהוא המסלול הקצר ביותר בין שתי נקודות במישור. בכדי לא לסבך, נבחר בתור הקשתות שלנו מקטעים על קווי אורך הנבדלים ב-90 מעלות, וכן קטע מקו המשווה (איור 2).

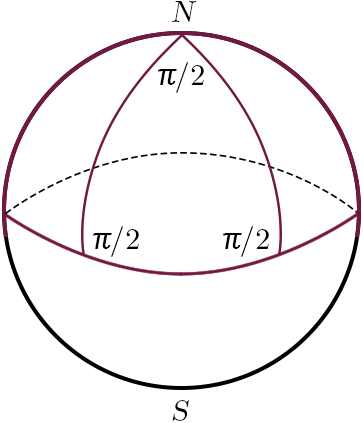
איור 2 – משולש כדורי שכל זוויותיו שוות ל-90 מעלות

סכום זוויות המשולש הכדורי דלעיל אינו שווה ל-$\pi$ אלא

\[\alpha + \beta + \gamma = \frac{3}{2}\pi \tag{1}\]

ניתן לבטא את העובדה שסכום הזוויות גדול מ-$\pi$ באמצעות השטח $S$ של המשולש הכדורי והרדיוס $R$ של הספירה:

\[\alpha + \beta + \gamma - \pi = \frac{S}{R^2} \tag{2}\]

ניתן להוכיח שהקשר הזה נכון לכל משולש כדורי באשר הוא. כמו כן, נשים לב שמהביטוי הזה אפשר לקבל גם את המקרה הרגיל של משולש במישור, אם נתייחס אל המישור כאל ספירה בעלת $R\to\infty$. את הנוסחה (2) אפשר לכתוב גם בצורה:

\[K=\frac{1}{R^2} = \frac{\alpha+\beta+\gamma-\pi}{S} \tag{3}\]

מכאן רואים שניתן להגדיר רדיוס של ספירה גם מבלי “לצאת” ממנה, כלומר מבלי להזדקק למרחב התלת-ממדי שבו היא חיה. לשם כך מספיק למדוד את שטח המשולש הכדורי ואת סכום זוויותיו. במילים אחרות, $K$ (או $R$) היא תכונה אינטרינזית (פנימית) של הספירה. לגודל $K$ נהוג לקרוא בשם עקמומיות גאוסית, וניתן להכליל אותה בנקל למשטח חלק שרירותי:

\[K(x) = \lim_{S \to 0} \frac{\alpha+\beta+\gamma-\pi}{S} \tag{4}\]

כאן הזוויות והשטח מתייחסים למשולש קטן הנמצא על המשטח, שתחום על ידי עקומים המתאימים למרחקים הקצרים ביותר על המשטח, והעקמומיות, באופן כללי, משתנה מנקודה לנקודה, כלומר היא גודל מקומי. במקרה כללי זה, בדיוק כמו במקרה של ספירה, $K$ היא תכונה אינטרינזית של המשטח, שאיננה תלויה בעובדה שהמשטח שקוע בתוך מרחב תלת-ממדי. עמקומיות גאוסית לא משתנה אם מכופפים את המשטח מבלי למתוח או לקרוע אותו. כך למשל, באמצעות כיפוף ניתן להפוך גליל או קונוס למישור, מה שאומר שעבור צורות אלה $K=0$ (כמו עבור מישור).

כעת נסתכל על הקשרים (3) ו-(4) מזווית אחרת. נחזור לאיור 2 ונבצע בו מספר שינויים. תחילה, נצייר בקוטב וקטור שיהיה בכיוון אחד משני קווי האורך. נתחיל להניע אותו לאורך אותו קו האורך, מבלי לשנות את הזווית ביניהם (שבמקרה זה שווה לאפס), עד שנגיע לקו המשווה. לאחר מכן נזיז אותו על קו המשווה – שוב מבלי לשנות את הזווית (כעת היא שווה $\pi/2$) – עד שנגיע לקו האורך השני. לבסוף, בדיוק באותו האופן נזיז את הווקטור על קו האורך השני עד שנגיע לקוטב שממנו התחלנו את התנועה (איור 3). התהליך שביצענו נקרא העתקה מקבילה. אילו התנועה הייתה מתרחשת לאורך מסלול סגור במישור, היינו מצפים שהווקטור בסוף התהליך היה מתלכד עם הווקטור בתחילת התהליך. אבל כאן, כפי שניתן לראות, זה לא קורה – הווקטור הסופי יוצר זווית של $\pi/2$ עם הווקטור ההתחלתי.

ניתן לבטא זאת גם באופן הבא:

\[\alpha + \beta + \gamma - \pi = KS \tag{5}\]

כלומר השינוי בזווית כתוצאה מגרירה של וקטור לאורך מסלול סגור (באופן שתואר לעיל) פרופורציונלי לשטח שתוחם המסלול. תוצאה זו פותחה עבור משטח דו-ממדי, אך ניתן להכלילה גם למרחבים לא-אוקלידים רב-ממדיים. אולם במקרה של מרחב $n$-ממדי, לא ניתן להסתפק בגודל סקלרי אחד $K(x)$ לתיאור העקמומיות. במקרה זה משתמשים באובייקט גאומטרי הרבה יותר מסובך שמכיל $n^2 (n^2 – 1)/12$ רכיבים. לאובייקט זה קוראים טנזור העקמומיות של רימן, והמרחבים הללו נקראים מרחבי רימן. לטנזור העקמומיות במרחב-זמן (מרחב רימן 4-ממדי) שבו משתמשים ביחסות כללית יש 20 רכיבים בלתי תלויים.

גודל נוסף שמופיע במשוואות השדה הגרביטציוני הוא טנזור תנע-אנרגיה. מדובר באובייקט גאומטרי המתאר את הצפיפות ואת שטף האנרגיה והתנע של חומר (ובאופן כללי של שדות שאינם גרביטציוניים). כידוע, אנרגיה היא גודל סקלרי בעוד שצפיפות שטף האנרגיה הוא גודל וקטורי. אין זה מפתיע אפוא כי צפיפות שטף התנע (כשלעצמו וקטור) הוא גודל טנזורי. משוואת איינשטיין המקשרת בין הגדלים שהוזכרו נראית כך

\[R_{ik} - \frac{1}{2} R g_{ik} + \Lambda g_{ik} = \frac{8 \pi G}{c^4} T_{ik}\]

כאשר $R_{ik}$ הוא טנזור ריצ’י (המתקבל מטנזור העקמומיות של רימן על ידי פעולת כיווץ – מן “מכפלה סקלרית” בין טנזורים) , $T_{ik}$ – טנזור תנע-אנרגיה, $g_{ik}$ – הטנזור המטרי (אוסף של גדלים המגדירים את התכונות הגאומטריות של המרחב), $R$ – גודל סקלרי הנקרא סקלר ריצ’י, $G$ – קבוע הכבידה העולמי, $c$ – מהירות האור בריק ו- $\Lambda$ – קבוע בעל ממדים של $\mathrm{m^{-2}}$ המכונה “הקבוע הקוסמולוגי” (זניח עד לסקלות של צבירי גלקסיות אך משחק תפקיד חשוב בקוסמולוגיה).

חשוב להדגיש כי יחסות כללית מדברת על עיקום המרחב-זמן, ולא רק המרחב. יותר מזה, כאשר מדובר במקורות כבידה כמו השמש או כדה”א, דווקא עקמומיות הזמן היא הדומיננטית.

לדוגמה, נראה כי במערכת המעבדה, למסלולים של כדור טניס וקליע המוצגים באיור הבא יש עקמומיות שונה:

מנקודת מבט של צופה במערכת המעבדה, למסלולים המרחביים של כדור הטניס והקליע עקמומיות שונה

אולם למעשה אין להם שום עקמומיות – המרחב-זמן בו הם שוהים בעצמו מעוקם כך שבפועל המסלולים שלהם ישרים (הם נקראים מסלולים גיאודזים).

ניסויים קלאסיים לאישוש יחסות כללית

בחלק הקודם הוזכר כי אין גופים שלא מושפעים משדה הכבידה. הדבר נכון גם עבור אור. בפרט, פוטון הנע בשדה כבידה מבצע עבודה כנגד כוח המשיכה וכתוצאה מכך מאבד אנרגיה. כידוע, אנרגיה של פוטון פרופורציונלית לתדירות, ולכן התדירות יורדת במהלך התנועה בשדה כבידה. איינשטיין חזה אפקט זה, הידוע בשם הסחה לאדום (או היסט לאדום), עוד בשנת 1907. ננסה להעריך עתה את גודל האפקט. עבודה כנגד כוח הכובד פרופורציונלית ל-$gh$, כאשר $g$ – תאוצת הנפילה החופשית ו-$h$ – הגובה. למכפלה $gh$ ממדים של ריבוע המהירות. לכן משיקולים של ממדים נסיק כי ההיסט היחסי של התדירות הוא:

\[\frac{\Delta \omega}{\omega} = \frac{gh}{c^2} \tag{6}\]

כאשר $c = 3 \cdot 10^{10} ~ \mathrm{cm/s}$ – מהירות האור בריק. עבור $g \approx 10^3 ~ \mathrm{cm/s^2} , h \sim 10^3~\mathrm{cm}$ מקבלים ערך זניח של ההיסט היחסי $\sim 10^{-15}$. לא מפתיע אפוא כי עברו כמעט 50 שנה עד שהצליחו להבחין באפקט הזה בניסוי. עשו זאת הפיזיקאים האמריקאיים רוברט פאונד וגלן רבקה, בניסוי המפורסם שלהם (ניסוי פאונד-רבקה) בעזרת טכנולוגיה חדשנית שהייתה מבוססת על אפקט מסבאואר.

אפקט נוסף שמנבאת יחסות כללית – סטייה של קרני אור בשדה הכבידה של השמש. גם אותו אפשר להעריך בצורה פשוטה יחסית. אם קרן האור עוברת במרחק (אופייני) $\rho$ מהשמש, הרי שהתאוצה הרדיאלית שווה $GM/\rho^2$, כאשר $G$ – קבוע הכבידה העולמי ו-$M$ – מסת השמש. בזמן אופייני $\rho/c$ הרכיב הרדיאלי של מהירות הפוטון מספיק להשתנות ב-$\frac{GM}{\rho c}$, לכן זווית הסטייה היא

\[\theta \sim \frac{GM}{c^2 \rho}\]

נגדיר את הרדיוס הגרביטציוני (הידוע גם כרדיוס שוורצשילד), שהוא גודל שימושי ביחסות כללית, באופן הבא:

\[r_g = \frac{2GM}{c^2} \tag{7}\]

אם כן, השיקולים החצי-קלאסיים הנאיביים שלנו נותנים

\[\theta = \frac{r_g}{\rho}\]

זוהי באמת התוצאה שקיבל איינשטיין באחת מהגרסאות הראשונות של יחסות כללית. ואולם מאוחר יותר התברר כי התוצאה הנכונה לפי יחסות כללית היא

\[\theta = 2\frac{r_g}{\rho} \tag{8}\]

הרדיוס הגרביטציוני של השמש הוא $r_g \approx 3 ~ \mathrm{km}$. הגיוני לבחור בתור המרחק $\rho$ (הקרוי גם פרמטר הפגיעה) ערך שקרוב לרדיוס השמש (השווה ל-$7\cdot 10^5 ~ \mathrm{km}$). אם נציב את המספרים ב-(8) נקבל שעבור קרן אור העוברת בקרבת השמש זווית הסטייה שווה בערך ${1.75}”$. המדידות שביצע ארתור אדינגטון בשנת 1919 במהלך ליקוי חמה אישרו זאת. זאת הייתה הצלחה גדולה של תורת היחסות הכללית.

אישור ניסיוני נוסף הגיע מחקירת הסטייה בפריהליון של כוכב חמה. במכניקה קלאסית, מסלול אליפטי סגור אופייני לתנועה בהשפעת פוטנציאל מושך מהצורה $1/r$. לא כך הדבר בתורת היחסות הכללית – מסלולים של כוכבי לכת אינם סגורים. נוח לתאר אפקט זה כסיבוב הפריהליון של מסלול אליפטי (איור 4). עוד הרבה לפני יחסות כללית אסטרונומים ידעו שהפריהליון של כוכב חמה מסתובב בערך ב-${6000}”$ בכל מאה שנים. סיבוב זה הוסבר כתוצר של ההשפעה הגרביטציונית מצד כוכבי לכת אחרים במערכת השמש. אולם גם אם מתחשבים בהשפעה זו, עדיין נשאר עודף לא מוסבר של בערך ${40}”$. בשנת 1915 איינשטיין הסביר את מקור הפער בעזרת תורת היחסות הכללית.

איור 4 – פרצסיית המסלול של כוכב חמה סביב השמש (באדיבות ויקימדיה)

משיקולים פשוטים של ממדים אפשר לצפות לכך שבסיבוב אחד, הסחת הפריהליון תהיה

\[\delta\sim\frac{r_g}{R}\]

כאשר $R$ – רדיוס המסלול. חישוב מדויק במסגרת יחסות כללית עבור מסלול שצורתו קרובה לצורה מעגלית נותן

\[\delta = \frac{3 \pi r_g}{R} \tag{9}\]

אם נציב את רדיוס המסלול של כוכב חמה ($R \approx 0.6 \cdot 10^8 ~ \mathrm{km}$) נקבל את הגודל ${43}”$ פר מאה שנה, מה שמסביר את הפער. ברור גם מדוע התופעה בולטת דווקא במקרה של כוכב חמה: זוהי הפלנטה הקרובה ביותר לשמש, כלומר עם רדיוס המסלול $R$ הכי קטן, ולכן עבורה הסחת הפריהליון היא מקסימלית.

חורים שחורים

תפקידה של יחסות כללית לא מסתכם בחקירת תיקונים קלים לתורת הכבידה הניוטונית. קיימים אובייקטים שבהם אפקטים של יחסות כללית משחקים תפקיד מרכזי. הם נקראים חורים שחורים.

עוד במאה ה-18, ג’ון מיצ’ל ופייר סימון לפלס הגו באופן בלתי תלוי את הרעיון לפיו קיימים כוכבים עם התכונה המוזרה הבאה: אור לא יכול לעזוב את פני השטח שלהם. מהלך המחשבה שלהם היה כזה. גוף בעל מהירות רדיאלית $v$ יכול להשתחרר משדה הכבידה של כוכב שרדיוסו $R$ ומסתו $M$ בתנאי שהאנרגיה הקינטית $mv^2/2$ שלו גדולה מאנרגיית המשיכה $GMm/R$, כלומר כל עוד $v^2 > 2GM/R$. אם נשתמש באי-שוויון זה עבור האור (כיום ברור שאין לכך שום ביסוס), נוכל להסיק שאם רדיוס הכוכב קטן מהערך

\[r_g = \frac{2GM}{c^2}\]

הרי שהאור לא יכול להשתחרר מפני הכוכב! באופן מפתיע, הקריטריון הזה שפותח משיקולים נאיביים, זהה כמותית לקריטריון שמתקבל במסגרת תורת היחסות הכללית. נשים לב גם כי הגודל $r_g$ הוא רדיוס שוורצשילד שכבר הוזכר קודם לכן בהקשר אחר (ראו נוסחה (7)).

חורים שחורים נוצרים בתהליך המכונה קריסה כבידתית – כוכב מתכווץ עד שבשלב מסוים השדה הגרביטציוני בקרבת הכוכב הוא כה חזק ששום דבר לא יכול לברוח ממנו – אפילו לא אור. מכאן ששום אינפורמציה לא יכולה לעזוב חור שחור. מחזה לא פחות מרהיב – נפילה של גוף לתוך חור שחור. מחד גיסא, מנקודת מבטו של צופה הנמצא במרחק אינסופי, הגוף הזה אף פעם לא ישיג את רדיוס שוורצשילד. מאידך גיסא, לפי השעון של צופה במערכת הצמודה לגוף עצמו, הוא ישיג את רדיוס שוורצשילד בזמן סופי.

אך אין לחשוב כי חורים שחורים הם סתם המצאה של תאורטיקנים. תצפיות אסטרונומיות רבות מצביעות על כך שמדובר באובייקטים אמיתיים. כך למשל, פרויקט בינלאומי בשם Event Horizon Telescope (או בקיצור EHT) שם לעצמו למטרה לחקור חורים שחורים על-מסיביים במרכזי גלקסיות. כיום בפרויקט משתתפים 11 מצפי כוכבים מיבשות שונות. באפריל של 2017, EHT ביצעו תצפיות של סגיטריוס A* – אובייקט קומפקטי הנמצא במרכז גלקסיית שביל החלב שפולט גלי רדיו. הוא מורכב מחור שחור שמסתו גדולה בערך פי $4\cdot 10^6$ ממסת השמש ומגרעין הגלקסיה האליפטית הענקית M87, שמכיל חור שחור בעל מסה הגדולה פי מיליארדים ממסת השמש.

בדיוק שנתיים אחרי תחילת התצפיות, צוות הפרויקט פרסם את התוצאות. בפרט, הוצגה לראשונה תמונה של חור שחור (ראה תמונה ראשית). בד בבד פורסמו שישה מאמרים ב-Astrophysical Journal Letters עם הסברים מפורטים אודות תהליך עיבוד הנתונים. המאמר הראשון מכיל מספר שחזורים גרפיים (אשר בוצעו בעזרת אגלוריתמים מיוחדים) של הצל הנגרם מהחור השחור. שאר המאמרים מכילים פרטים טכניים שונים וכן סקירה של מודלים תיאורטיים שבהם השתמשו החוקרים לעיבוד התוצאות.

פולסר PSR 1913+16 וגלי כבידה

בשנת 1993 שני פיזיקאים אמריקאיים, הולס וטיילור קיבלו פרס נובל בפיזיקה על חקירת הפולסר PSR 1913+16 (כאן PSR הוא קיצור של פולסר והמספרים מתארים את הקואורדינטות שלו במערכת השמימית: עלייה ישרה של $19^{\mathrm{h}}13^{\mathrm{m}}$ ונטייה של $+16^{\circ}$). מחקירת ספקטרום הפליטה שלו התברר כי הוא חלק ממערכת כפולה. במילים אחרות, לפולסר הזה יש שותף, ושניהם מסתובבים סביב מרכז המסה של המערכת. המרחק הממוצע ביניהם הוא מסדר גודל של $2\cdot 10^6 ~ \mathrm{km}$. אילו השותף היה כוכב רגיל עם רדיוס אופייני של $\sim 10^6 ~ \mathrm{km}$, הרי שניתן היה להבחין בליקוי הפולסר. אולם זה לא קורה. מניתוח התצפיות התברר כי השותף הזה אינו אלא כוכב נייטרונים.

קיומם של כוכבי נייטרונים נובא באופן תיאורטי עוד בשנות ה-30. הם נוצרים כתוצאה מקריסה כבידתית מהירה של כוכבים מסיביים, שמלווה בפיצוץ סופרנובה. לאחר הפיצוץ הלחץ בליבה הנותרת ממשיך לגדול, מה שגורם לאלקטרונים ולפרוטונים להתמזג ולהפוך לנייטרונים (תוך פליטה של נייטרינו). כתוצאה, מתקבל כוכב בעל צפיפות גבוהה – מסתו גדולה במקצת ממסת השמש אך הוא קטן מאוד מבחינת הממדים שלו – סדר גודל של $10 – 15 ~\mathrm{km}$, כלומר לא גדול יותר מאסטרואיד. גילוי של כוכב נייטורנים הוא, כמובן, הישג בפני עצמו.

נוסף על כך, ניתוח קפדני של תנועת המערכת הכפולה הזאת הניב אישור נוסף לכך שהמסלולים האליפטיים אינם סגורים, כפי שנובע מיחסות כללית. היות ובמערכת הזאת השדה הגרביטציוני מאוד חזק, הפריאסטרון מסתובב במהירות הרבה יותר גדולה מאשר הפריהליון של כוכב חמה – ההסחה של הפריאסטרון היא בערך $4.2^{\circ}$ לשנה! חקר תופעה זו (ותופעות אחרות) סייעו בקביעת מסת הפולסר וכוכב הנייטרונים – הם שווים 1.441 ו-1.387 מסות השמש בהתאמה. אך זה עדיין לא הכול.

בשנת 1918, באמצעות תורת היחסות הכללית, איינשטיין ניבא את קיומם של גלי כבידה – גלים המתפשטים במרקם המרחב-זמן. כידוע, כאשר מאיצים חלקיקים הטעונים חשמלית הם פולטים קרינה אלקטרומגנטית. באופן אנלוגי, גופים בעלי מסה פולטים גלי כבידה המתפשטים במהירות האור. אולם האנלוגיה הזאת לא מלאה. אחד ההבדלים המשמעותיים ביותר שקיימים בין גלים אלקטרומגנטיים וגלי כבידה קשור לעניין של צפיפות אנרגיה. בניגוד לשדה אלקטרומגנטי, צפיפות האנרגיה של שדה גרביטציוני בנקודה נתונה תמיד ניתנת לאיפוס באמצעות בחירה מתאימה של מערכת קואורדינטות. זוהי תוצאה ישירה של עקרון השקילות. כמו שכבר אמרנו, במעבר למערכת ייחוס הצמודה למעלית שנופלת חופשית, אנחנו אפקטיבית “מעלימים” את שדה הכבידה. ואם עוצמת השדה שווה לאפס, אין פלא שגם צפיפות האנרגיה באזור זה שווה לאפס. מה שחשוב כאן זה שהאנרגיה הכוללת והתנע הכולל הם גדלים בעלי משמעות פיזיקלית אמיתית (כמובן בתנאי שהשדה דועך מספיק מהר באינסוף).

כל זה לא אומר שגלי כבידה הם אבסטרקציה מתמטית. מדובר בתופעה פיזיקלית לכל דבר, ובאופן עקרוני ניתן לצפות בה. למשל, אם נציב מוט בשדה כבידה, גלי הכבידה שיפגעו בו יגרמו לדפורמציות שישתנו עם התדירות. אולם האמירה “באופן עקרוני” איננה מקרית כאן. האובייקטים שסביבנו אינם כבדים או מהירים מספיק בכדי שיהיה אפשר להבחין בגלי הכבידה שהם יוצרים. בכדי ליצור גל חזק, צריך לטלטל באופן משמעותי את מארג המרחב-זמן. המועמד האידאלי לתפקיד זה – מערכת של שני חורים שחורים, המסתובבים זה סביב זה במרחק קטן (מסדר גודל הרדיוס הגרביטציוני שלהם). עיוות המטריקה יהיה כה גדול שחלק מהאנרגיה של הזוג הזה תיפלט בצורה של גלי כבידה. כתוצאה מאיבוד האנרגיה המרחק יקטן ובד בבד תגדל מהירות הסיבוב, מה שיגרום לעיוות גדול יותר של המרחב-זמן שבתורו יגרום לפליטה של גלי כבידה חזקים עוד יותר. בשלב מסוים החורים השחורים יתמזגו, מה שיתבטא בפיצוץ עצום. אך האנרגיה לא תיפלט בצורה של אור, או חלקיקים כלשהם, אלא בצורה של תנודות במרחב-זמן. מדובר בכמות עצומה של אנרגיה שתשתחרר בשבריר של שנייה. תנודות דומות יכולות להיווצר גם כתוצאה ממיזוג של כוכבי נייטרונים. תהליכים אחרים כמו קריסת ליבה של כוכב (סופרנובה) גם הם יגרמו לפליטה של גלי כבידה, אם כי בעוצמה קצת יותר חלשה.

בכל אופן, התנודות הללו יתפשטו לכל הכיוונים. משרעת התנודות תקטן ככל שנתרחק ממקור הפיצוץ, וכאשר ההד ישיג את כדה”א ההעתק היחסי של הגופים שיושפעו מהתנודות יהיה מסדר גודל של $10^{-22}$ או פחות.

כמובן שאם המיזוג יתרחש בגלקסיה שלנו, הרעידה במרחב-זמן שתגיע לכדה”א תהיה הרבה יותר חזקה. אולם אירועים כאלה מתרחשים רק פעם בכמה אלפי שנים. לכן אם אנחנו רוצים להבחין בגלי כבידה, צריך שהגלאי שלנו יהיה מסוגל להרגיש מיזוג של כוכבי נייטרונים או חורים שחורים במרחקים של עשרות או אלפי מגה-פארסק (כלומר עליו לכסות מיליוני גלקסיות). כמו שאפשר לנחש, בנייה של גלאי רגיש שכזה היא משימה מורכבת. אך לפני שנעבור לסקירה היסטורית קצרה בנושא, נחזור לפולסר PSR 1913+16. מכל האמור לעיל נובע שהמערכת הכפולה הזאת צריכה לפלוט גלי כבידה. מדובר באנרגיה עצומה – מסדר גודל האנרגיה הכוללת שפולטת השמש. נשמע מרשים, אך גם זה לא מספיק בשביל להבחין בגלי הכבידה כאן, על כדה”א. יחד עם זאת, כמו שכבר אמרנו, אנרגיית גלי כבידה יכולה לבוא על חשבון אנרגיית התנועה של הכוכבים, והפחת באנרגיית התנועה גורם להקטנה במרחק בין הכוכבים. ממדידת ספקטרום הקרינה האלקטרומגנטית (בתחום הרדיו) המגיעה מהפולסר PSR 1913+16 התברר כי המרחק בין הכוכבים במערכת הכפולה הזאת אכן קטן בכמה מטרים בכל שנה, בדיוק כפי שמנבאת תורת היחסות הכללית.

ניסוי LIGO

החיפושים אחר גלי כבידה התחילו עוד בשנות ה-60 ומהר מאוד התרחשה סנסציה. הפיזיקאי ג’וזף ובר מאוניברסיטת מרילנד בנה את גלאי התהודה הראשון בעולם. הוא היה מורכב מגליל אלומיניום באורך 2 מטרים המבודד מרטט חיצוני שאל המעטפת שלו חוברו חיישנים פיזואלקטריים רגישים. גלי הכבידה פוגעים בגליל ומעוררים בו תנודות תהודה אותן אמורים לקלוט החיישנים. ובר בנה מספר גלאים כאלה, ובשנת 1969 הוא הודיע באופן חגיגי כי הצליח להבחין בגלי כבידה במספר גלאים בבת אחת. הוא טען שמשרעת התנודות שהתקבלה הייתה מסדר גודל של $10^{-16}$, כלומר פי מיליון מהערך המצופה. הקהילה המדעית הטילה ספק באמינות טענותיו, בייחוד לאור העובדה שקבוצות מחקר אחרות שבנו גלאים דומים לא הצליחו להבחין באות כה חזק. אף על פי כן, הניסוי הזה של ובר עזר להאיץ את המחקר בתחום. מדענים שעבדו על שיפור המערכת של ובר הצליחו להקטין משמעותית את השפעת הרעשים החיצוניים בעזרת קירור. אך עדיין הדיוק לא היה טוב מספיק וספקטרום התהודה של המערכת היה צר מדי.

אלא שהיו פרויקטים הרבה יותר מבטיחים שהתבססו על רעיון מעט שונה. במקום למדוד תנודות של גוף אחד כלשהו, אפשר למדוד שינוי במרחק בין שני עצמים תלויים – למשל בין שתי מראות. גלי הכבידה יגרמו לתנודות במרחב מה שיעורר תנודות קטנות גם במרחק. קרן לייזר הכלואה בין המראות תושפע מהתנודות הללו. מערכת כזאת מסוגלת לזהות תנודות בטווח רחב של תדירויות, מ-10 הרץ ועד 10 קילו-הרץ, וזה בדיוק טווח התדירויות של הקרינה הנפלטת מכוכבי נייטרונים מתמזגים.

המימוש המודרני של הרעיון הנ”ל, המבוסס על אינטרפרומטר מייקלסון, מוצג באיור 5. בתוך שני תאי ואקום (באורך של מספר קילומטרים) המאונכים זה לזה תלויות מראות. בכניסה למערכת קרן הלייזר מתפצלת לשתי קרניים שעוברות דרך התאים, מוחזרות מהמראות ומתאחדות שוב לקרן אחת. מקדם האיכות של המערכת הוא כה גבוה שמתרחשות הרבה פגיעות והחזרות. האורכים נבחרו כך שבהיעדר עירור חיצוני, הקרניים ביציאתן מההתקן מבטלות זו את זו בכיוון הגלאי כך שמתקבל צל ועל כן לא נקלט שום אות. אך מספיקה תזוזה קטנה של המראות בהשפעת גלי הכבידה בכדי להפר את האיזון הדק ולגרום לאור לפגוע בגלאי. וככל שהתזוזה גדולה יותר כך גם חזקה יותר עוצמת האור הנקלטת.

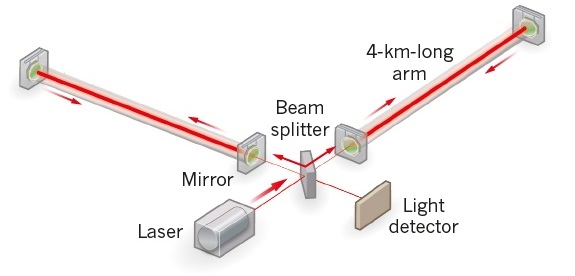
איור 5 – מדידת גלי כבידה באמצעות אינטרפרומטר. גלי הכבידה משנים את אורכי הזרועות הנמצאים באנטי-פאזה מה שמבטל את ההתאבכות ההורסת וגורם לגלאי האור לקלוט אות
(מתוך D. Castelvecchi & A. Witze, 2016. Einstein's gravitational waves found at last)

הביטוי “תזוזה קטנה” לא מתאר מספיק טוב עד כמה המערכת רגישה. לדוגמה, אפשר להבחין בקלות בתזוזה של מראות במרחק של אורך גל אינפרא-אדום (סדר גודל של מיקרונים). היות ואורך הזרועות הוא 4 ק”מ מדובר בתזוזות המתאימות לתנודות במרחב-זמן עם משרעת של $10^{-10}$. ניתן להבחין בלי בעיה גם בתזוזות במרחק של קוטר האטום – בסך הכול קרן הלייזר צריכה לטייל הלוך וחזור מספיק פעמים בכדי לצבור הפרש פאזה מתאים. אך גם בסקלה כזאת מקבלים משרעת מסדר גודל של $10^{-14}$ בלבד (וגם זה בקושי). כדי להגיע לסדרי גודל כמו $10^{-22}$ צריך להיות מסוגלים להבחין בתזוזות של אלפית קוטר האטום!

בכדי להגיע לרמות דיוק פנומנליות כאלה הפיזיקאים היו צריכים להתגבר על מכשולים רבים. חלקם היו מכניים: למשל בכדי להיפטר מרעשים היה צריך לתלות מראות כבדות על שרשרת של סיבים. חלקם היו אופטיים: ככל שקרן האור יותר חזקה כך ניתן להבחין בתזוזות קטנות יותר. אולם הגדלת העוצמה גרמה להתחממות לא אחידה של האלמנטים האופטיים, מה שפגע בתכונות הקרן.

מעבדות רבות השתתפו במרוץ הזה, כאשר מעבדת ה-LIGO הייתה המובילה. LIGO היא יוזמה של שלושה מדענים מ-MIT ומ-Caltech: ריינר וייס (Rainer Weiss) שמימש את רעיון הגלאי האינטרפרומטרי לזיהוי גלי כבידה, רונלד דרבר (Ronald Drever) אשר הצליח להשיג יציבות מספיקה של קרן האור על מנת לקלוט את האות וקיפ תורן (Kip Thorne) – תאורטיקן הידוע לקהל הרחב גם כמי ששימש יועץ מדעי לסרט “בין כוכבים”.

פרויקט LIGO החל לפעול בשנת 2002 ועד לשנת 2010 הספיק לערוך שש תצפיות, שאמנם לא הובילו לזיהוי גלי כבידה – הפיזיקאים רק הצליחו לתת חסם עליון לתדירות האירועים הללו. זה לא מאוד הפתיע אותם כי לפי כל ההערכות הסיכוי להתפרצות משמעותית באותו האזור ביקום שסרק הגלאי היה נמוך (בערך רק פעם בכמה עשורים).

בשנים 2010-2015 שיתוף הפעולה בין LIGO ו-Virgo הביא לשיפור משמעותי במכשור. כעת קליטת גלי הכבידה נראתה ריאלית מתמיד. LIGO – וליתר דיוק, aLIGO (כלומר Advanced LIGO) – הייתה מוכנה לזהות התפרצויות של כוכבי נייטרונים במרחק של 60 מגה-פארסק ושל חורים שחורים במרחק של מאות מגה-פארסק. נפח היקום שניתן היה להאזין לו גדל באופן משמעותי.

אמנם לא ניתן לנבא במדויק היכן ומתי יתרחש “פיצוץ גרביטציוני”, אך רגישות הגלאים החדשים הייתה כה גבוהה שאפשר היה לצפות לזיהוי אירוע של מיזוג כוכבי נייטרונים כבר ב-4 החודשים הראשונים לתפעול המערכת. על אחת כמה וכמה כאשר מדובר בתצפיות שנמשכות מספר שנים: או שנקבל שלל של התפרצויות או שניאלץ להסיק כי קיימת בעיה רצינית בתורת היחסות הכללית.

התצפיות הראשונות החלו בספטמבר 2015 ונמשכו עד ינואר 2016. במקביל באינטרנט רצו שמועות על זיהוי גלי כבידה, אך צוות הפרויקט שמר על שתיקה והסתפק רק בהודעה קצרה לתקשורת: “אנו אוספים ומנתחים את הנתונים ובשלב זה לא מוכנים להודיע על התוצאות”. העובדה שבשלב העיבוד אנשי הצוות בעצמם אינם יכולים להיות בטוחים בכך שמה שהם רואים הוא אכן גל כבידה תרמה גם היא לאינטריגה. העניין הוא שפרוייקט LIGO בנוי כך שמדי פעם מערכת ממוחשבת מזריקה אירועי התפרצות מלאכותיים לתוך שטף הנתונים. הפרוצדורה נקראת “הזרקה עיוורת” (blind injection) ומתוך כל הצוות רק לשלושה אנשים יש גישה למערכת (אשר מבצעת את ההזרקות שרירותית). הצוות צריך לזהות את האירוע, לעבד את הנתונים ורק בשלב האחרון ייוודע אם מדובר באירוע אמיתי או בתרגיל שנועד לבדוק ערנות. אגב, ב-2010 כבר קרה מקרה כזה והמדענים אף הספיקו לכתוב מאמר בטרם נודע להם שזאת הייתה הזרקה עיוורת.

לבסוף, ב-11 בפברואר 2016 זה קרה. צוות LIGO קיים מסיבת עיתונאים (ובמקביל פרסם מאמר ב-Physical Review Letters) שבה הוכרז על מדידת גלי כבידה. מה שמעניין הוא שהאירוע, שקיבל את הסימון GW150914, נקלט עוד ב-14 בספטמבר, כלומר ארבעה ימים לפני תחילת התצפית הרשמית, כשהגלאים כבר פעלו ורק נעשו בדיקות אחרונות. על מה שהתרחש באותם הימים מאחורי הקלעים ניתן לקרוא בכתבה הזאת.

עידוש כבידתי וננסים חומים

כזכור, גם קרני האור מושפעים מגרביטציה. על עובדה זו בדיוק מתבסס עידוש כבידתי – היות וקרני אור מתעקמות בקרבת כוכבים ניתן להתייחס אל הכוכבים כאל עדשות כבידה. את הרעיון הגו ארתור אדינגטון ואוליבר לודג’ בשנת 1919. עדשת כבידה למעשה משנה את מיקומו הנראה של הכוכב (המשמש כמקור אור) ביחס למיקומו האמיתי.

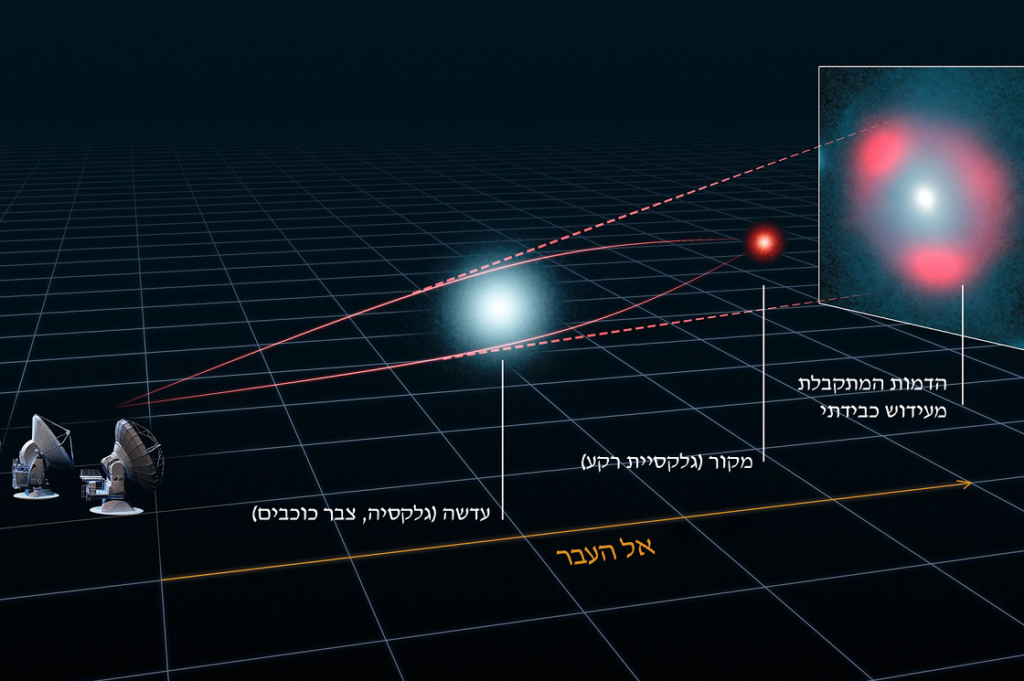
אופן הפעולה של עדשת כבידה (באדיבות space.com)

הערכה ראשונית גסה על סמך שיקולים של ממדים מובילה למסקנה כי הדמות נמצאת בזווית של $r_g/d$ ביחס למקור, כאשר $r_g$ – הרדיוס הכבידתי של העדשה, ו-$d$ – המרחק האופייני בבעיה. במקרה זה, אפילו אם היינו לוקחים בתור העדשה שלנו צבר של $10^4$ כוכבים ובוחרים $d \sim 10 ~\mathrm{ly}$ (ly – light years), היינו מקבלים זווית של $10^{-10} ~ \mathrm{rad}$ בלבד. ברור שלא ניתן להבחין בזווית שכזו בניסוי.

אולם זוהי הערכה שגויה. ניווכח בכך בעזרת הדוגמה הפשוטה הבאה. מדובר בבעיה ידועה שהוצגה על ידי הפיזיקאי אורסט חבולסון בשנת 1924 בכתב העת “Astronomische Nachrichten”. היא נבחנה שוב על ידי איינשטיין בשנת 1936. באיור 6 מתוארת עדשה $L$, מקור אור $S$ וצופה (מסך) $O$ – כולם על אותו ציר. נסמן ב-$d_1$ את המרחק בין המקור לעדשה, ב-$d$ את המרחק בין העדשה לצופה וב-$r_g$ את הרדיוס הכבידתי של העדשה (כוכב או צבר של כוכבים).

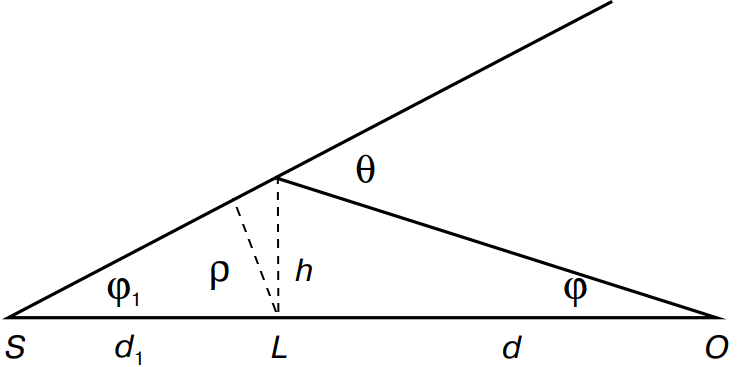
איור 6 – מערכת בעלת סימטריה צירית

ברור שלכל ערכי $d_1$, $d$ ו-$r_g$ אפשר למצוא מרחק מינימלי $\rho$ בין קרן האור לבין העדשה כך שהאור יפגע במסך. ברור גם שהתמונה שמתקבלת על המסך היא טבעת שאותה רואה הצופה בזווית של $\varphi$. הזוויות $\varphi$ ו-$\varphi_1$ הן כה קטנות שאפשר לקרב אותן על ידי הביטויים $\varphi=h/d$, $\varphi_1 = h/d_1$. כמו כן, מתקיים $h=\rho$. מכאן נובע כי

\[\theta = \varphi + \varphi_1 = \frac{h(d_1+d)}{d_1d}\]

מצד שני, אם נבטא את $\theta$ בעזרת נוסחה (8) נקבל:

\[h = \sqrt{2r_g\frac{d_1d}{d_1+d}}\]

לפיכך

\[\varphi = \sqrt{2r_g\frac{d_1}{(d_1+d)d}} \tag{10}\]

אם כן, סדר הגודל הנכון הוא $\sqrt{r_g/d}$ ולא $r_g/d$ כמו שקיבלנו בהתחלה (אנו מניחים כי כל המרחקים הם מאותו סדר גודל). יש הבדל משמעותי בין סדרי הגודל הללו ולא ניתן עוד לטעון כי האפקט זניח.

ניתחנו את המקרה שבו יש סימטריה צירית (המקור, העדשה והמסך ממוקמים על אותו הציר) והתמונה שמתקבלת על המסך היא, כאמור, טבעת – נהוג לקרוא לה טבעת איינשטיין. אמנם קשה למצוא מערכת אידאלית שבה המקור, העדשה והצופה נמצאים בדיוק על ציר אחד, אבל קיימות מערכות שמאוד קרובות למצב הזה. להלן שתי דוגמאות לאובייקטים כאלה:

טבעות איינשטיין שצולמו על ידי טלסקופ החלל האבל (באדיבות NASA, ESA, A. Bolton (Harvard-Smithsonian CfA) and the SLACS Team)

אולם התמונה משתנה אם עדשת הכבידה לא נמצאת על הישר המחבר את המקור עם המסך. במקרה של עדשה בעלת סימטריה כדורית נוצרות שתי דמויות (איור 7) – האחת נמצאת בתוך טבעת איינשטיין (שהייתה נוצרת אילו הייתה סימטריה צירית), והשנייה מחוץ לה.

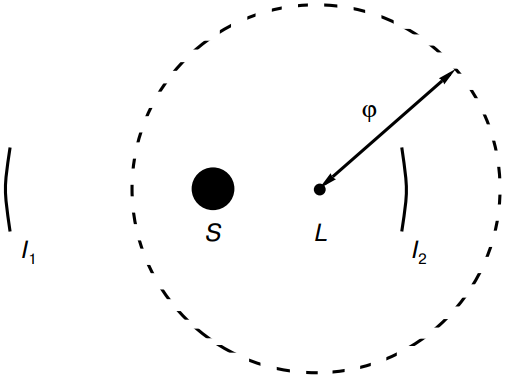
איור 7 – המקרה הכללי של עידוש כבידתי. $S$ – היטל המקור על המישור הקדמי, $L$ – היטל העדשה, $I_1,I_2$ – הדמויות שמתקבלות

דוגמה למערכת כזאת היא זוג הקוואזרים Q0957+561, כאשר העדשה היא הגלקסיה האליפטית YGKOW G1:

כתוצאה מעידוש כבידתי מתקבלות שתי דמויות, למרות שבפועל יש רק קוואזר אחד (באדיבות Hubble/WikiSky)

תזוזה של מקור האור תגרור תזוזה של שתי התמונות. אם עוצמות ההארה של התמונות מאותו סדר גודל כמו עוצמת ההארה של המקור אפשר עדיין להשתמש בנוסחה (10). אם מסת הכוכב, שמשחק את תפקיד העדשה, היא קטנה, למשל פי 2-3 סדרי גודל ממסת השמש, הרי שהזווית שתתקבל תהיה $\sim 0.001^{\prime\prime}$, דהיינו זווית שכמעט בלתי אפשרי להבחין בה. ועדיין, קיימת דרך להבחין באפקט. העניין הוא שכאשר מקרבים את התמונות, עוצמת ההארה הכוללת שלהן גדלה. אפקט זה נקרא מיקרו-עידוש (microlensing) ויש לו את התכונה המעניינת הבאה: השינוי בעוצמת ההארה מתרחש באופן סימטרי בזמן ובלי תלות באורך הגל (הזווית בנוסחה (10) לא תלויה באורך הגל).

בשנות ה-90, שלוש קבוצות בולטות של אסטרונומים חיפשו מאורעות כאלה: MACHO (אוסטרליה-ארה”ב), EROS (צרפת) ו-OGLE (ארה”ב-פולין). הם לא רק הצליחו להבחין באפקט, אלא אף גילו סוג חדש של גרם שמים: ננסים חומים – הם אלה שמשחקים את תפקיד המיקרו-עדשה.

לסיכום

תורת היחסות הכללית היא תורה פיזיקלית שלמה – בדיוק כמו מכניקה קלאסית, אלקטרודינמיקה או מכניקה קוונטית, היא נותנת תשובות חד משמעיות לשאלות בעלות משמעות פיזיקלית. היא מנבאת בצורה מדויקת תוצאות של תצפיות ומדידות. אולם כמו לכל תאוריה פיזיקלית, יש לה את תחום היישום שלה. כך למשל, היא איננה ישימה במקרה של שדות גרביטציוניים חזקים (שם צריך להתחשב באפקטים קוונטיים). על אף המאמצים הרבים, אין עדיין תורת גרביטציה קוונטית קונסיסטנטית.

יחסות כללית היא תורה פיזיקלית מופלאה כי היא מבוססת למעשה על עקרון אמפירי אחד שהיה ידוע עוד הרבה לפני יצירתה (כל הגופים נופלים באותה התאוצה בשדה כבידה). היא מופלאה גם כי היא ברובה פרי עמלו של אדם אחד. אבל מעל הכול, יש לה יופי פנימי. לב לנדאו נהג לומר שפיזיקאי תיאורטיקן אמיתי הוא כזה שמתפעל מיופיה של יחסות כללית כבר אחרי היכרות ראשונית עימה.

בערך עד אמצע שנות ה-60 תורת היחסות הכללית לא ממש התפתחה – רוב הפעילות התמקדה בפתירת בעיות חשובות אך ספציפיות מאוד. ייתכן כי זה נבע מכך שהתיאוריה במובן מסוים הקדימה את זמנה. מצד שני, כבר בשנת 1915 איינשטיין פרסם אותה בצורתה הסופית. בנוסף, חשוב להבין שעד לאחרונה, הבסיס התצפיתי של יחסות כללית היה מאוד דל כי על מנת להבחין באפקטים יחסותיים נדרש דיוק רב. למשל, את אפקט ההסחה לאדום הצליחו למדוד רק 40 שנה אחרי שהבחינו בסטיית קרני אור בקרבת השמש. כיום המצב שונה בתכלית – תורת היחסות הכללית מפתחת בקצב מהיר הודות לתצפיות אסטרונומיות חדשות ושדרוג הכלים הניסיוניים.