בעזרת החוק השני של ניוטון ניתן להבין כיצד גופים נעים לפי הכוחות הפועלים עליהם (למשל, ניתן למצוא את תאוצת הגופים). אם יודעים את התאוצה ואת המסה, ניתן לקבוע את הכוח השקול הפועל על הגוף.

כאשר מרכיבים משוואות תנועה תחילה יש למצוא את כל הכוחות הפועלים על מסה נקודתית נתונה (כולל כוחות תגובה); לאחר מכן צריך למצוא את הכוח השקול (הסכום הווקטורי של כל הכוחות הנתונים). אחר כך יש לרשום את החוק השני של ניוטון: הכוח השקול שווה למסה כפול התאוצה. את המשוואה המתקבלת יש לפתור ביחס לגודל שאיננו ידוע.

מעלית מאיצה

על רצפת מעלית נמצא אדם אשר מסתו היא $m$. יש לקבוע עם איזה כוח האדם לוחץ על רצפת המעלית אם המעלית נעה:

א) אנכית מעלה עם תאוצה;
ב) אנכית מעלה עם תאוטה;
ג) אנכית מטה עם תאוצה;
ד) אנכית מטה עם תאוטה;
ה) במהירות קבועה

מכיוון שהאדם נח ביחס למעלית, הוא נע ביחס לכדור הארץ עם אותה התאוצה כמו של המעלית. מהחוק השלישי של ניוטון אנו יודעים כי רצפת המעלית מפעילה על האדם כוח ששווה בגודלו ומנוגד בכיוונו לכוח שמפעיל עליה האדם. אם כן, על האדם פועלים שני כוחות: כוח המשיכה $\mathbf{P}$ וכוח התגובה $\mathbf{Q}$ של רצפת המעלית (הנקרא גם הכוח הנורמלי).
נכוון את ציר $y$ אנכית כלפי מעלה. מכאן שלכוח התגובה סימן חיובי, לכוח המשיכה – שלילי, וסימן וקטור התאוצה משתנה ממקרה למקרה.

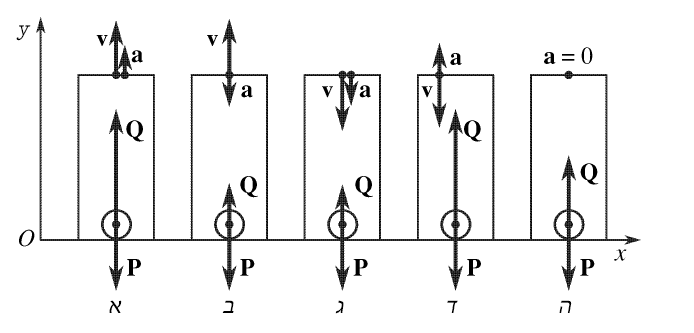
במקרה א’ וקטור התאוצה מכוון אנכית מעלה ולכן הוא חיובי; כך גם במקרה ד’ – וקטור התאוצה מנוגד לכיוון וקטור המהירות כאשר המעלית נעה בתאוטה. במקרים ב’ ו-ג’ וקטור התאוצה מכוון אנכית מטה.

משוואת התנועה תירשם בצורה וקטורית כך:

\[\mathbf{P}+\mathbf{Q}=m\mathbf{a}\]

בכדי לעבור לצורת כתיבה סקלרית, יש להתחשב בכיוון הווקטורים (סימן הרכיב הסקלרי של כל וקטור). עבור המקרים א’ ו-ד’: $-P+Q=ma$, כלומר

\[Q=P+ma=m(g+a)\]

עבור המקרים ב’ ו-ג’: $-P+Q=-ma$, ולכן

\[Q=m(g-a)\]

ועבור המקרה האחרון ה’: $-P+Q=0$, ומכאן

\[Q=P\]

כלומר, אם המעלית נעה ביחס לכדור הארץ בתאוצה (ובכך מהווה מערכת לא אינרציאלית), הכוח הנורמלי שמפעילה הרצפה איננו שווה לכוח המשיכה הפועל על הגוף. אם תאוצת המעלית מכוונת נגד תאוצת הנפילה החופשית, אז כוח התגובה של הרצפה גדול מכוח המשיכה. כאשר תאוצת המעלית היא בכיוון תאוצת הנפילה החופשית, הכוח הנורמלי קטן מכוח המשיכה. אם במקרה זה $a=g$, מהמשוואות הקודמות נובע כי $Q=0$, כלומר הגוף בכלל לא לוחץ על הרצפה. ורק כאשר המעלית נעה בתנועה קצובה ביחס לכדור הארץ (כמערכת ייחוס אינרציאלית), הכוח הנורמלי מתאזן עם כוח המשיכה.

מטוס המבצע לולאה

מטוס הנע במהירות $v$, מבצע לולאה בעלת רדיוס $r$. איזה כוח מפעיל הטייס על מושב המטוס? איזו מהירות מינימלית צריכה להיות לו בנקודה העליונה על מנת שהוא עדיין יהיה על המושב ולא יתנתק ממנו?

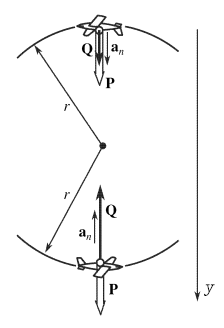
במקום למצוא את הכוח שבו הטייס לוחץ על המושב, אנו נמצא את כוח התגובה השווה לו בגודלו והמנוגד לו בכיוונו אשר מפעיל המושב על הטייס. על הטייס פועלים שני כוחות: כוח תגובה של המושב וכוח המשיכה מצד כדור הארץ. בנקודה התחתונה כוח התגובה מכוון אנכית כלפי מעלה, ובנקודה העליונה כוח התגובה של המושב מכוון אנכית מטה. אמנם המטוס נע במסלול מעגלי בתנועה קצובה, אך וקטור המהירות שלו כל הזמן משנה כיוון, ולכן קיימת תאוצה נורמלית (צנטריפטלית) השווה בגודלה $a_n=\frac{v^2}{r}$. בנקודה התחתונה ביותר היא מכוונת אנכית מעלה ובנקודה העליונה ביותר – כלפי מטה. נעביר את ציר $y$ לשם נוחות כך שכיוונו החיובי יצביע אנכית מטה, לאורך הכיוון של וקטור כוח הכובד.

משוואת התנועה בצורה וקטורית תירשם כך

\[\mathbf{P}+\mathbf{Q}=m\mathbf{a}_n\]

בפרוייקציות על ציר $y$ נקבל עבור הנקודה התחתונה את המשוואה $P-Q=-\frac{mv^2}{r}$ ולכן

\[Q=P+\frac{mv^2}{r}=m \left(\frac{v^2}{r} + g \right)\]

לכן, במקרה זה הטייס מרגיש עומס-יתר ($Q>mg$).

עבור הנקודה העליונה נקבל $P+Q=\frac{mv^2}{r}$, ומכאן

\[Q=\frac{mv^2}{r}-P=m \left (\frac{v^2}{r} - g\right )\]

מכיוון ש-$Q$ זה גודל כוח התגובה (אורך של וקטור), כלומר ערך גדול מאפס, הגודל $\frac{v^2}{r}$ לא יכול להיות קטן מ-$g$. כלומר, הטייס לא יתנתק מן המושב כל עוד $\frac{v^2}{r}\geq g$. המהירות המינימלית מתקבלת עבור ערך גבולי כאשר $Q=0$, כלומר

\[\frac{v^2}{r}-g=0\]

לכן המהירות המינימלית שצריכה להיות על מנת שהטייס לא יתנתק מהמושב היא

\[v_{min}=\sqrt{gr}\]

חוסר משקל

כידוע, משקל זהו כוח שמפעיל גוף על משטח כתוצאה מכוח המשיכה שפועל עליו (למשל בכדור הארץ). ראינו בדוגמאות הקודמות כי כאשר גוף נח ביחס לכדור הארץ, משקלו שווה לכוח המשיכה. בנוסף לכך, בדוגמה הראשונה ראינו כי משקלו של גוף שווה לכוח המשיכה גם במקרה של מעלית הנעה במהירות קבועה בקו ישר ביחס לכדור הארץ, כלומר במערכת אינרציאלית. לכן, ניתן לומר את הדבר הבא:

בכל מערכת אינרציאלית משקלו של גוף שווה לכוח המשיכה הפועל עליו.

אם גוף נמצא במעלית הנעה בתאוצה יחסית לכדור הארץ או במטוס הנע במסלול מעגלי (גם כן בתאוצה יחסית לכדור הארץ), הרי שמשקלו כבר לא שווה לכוח המשיכה.

נדון כעת במקרה בו אסטרונאוט נמצא בתוך חללית. איזה כוח הוא מפעיל על המושב שבו הוא יושב במקרה של המראה, בלימה ותנועה חופשית במסלול מעגלי סביב הארץ?

כאשר החללית ממריאה היא נעה בתאוצה בגלל השפעת הטיל המאיץ. המקרה הזה זהה לגמרי למקרה של המעלית במצב א’ שדנו בו בפסקה הקודמת. במקרה זה, האסטרונאוט מפעיל כוח על המושב שגדול יותר מכוח המשיכה המופעל עליו. לפי החוק השלישי של ניוטון, הכוח שהאסטרונאוט מפעיל על המשטח הינו $Q=m(g+a)$ בעוד שכוח המשיכה שווה ל-$mg$. האסטרונאוט ירגיש עומס יתר, כלומר הוא ירגיש שהוא נעשה כבד יותר.

גוף של אדם מאומן יכול להחזיק מעמד בעומס פי שש מהרגיל, כלומר $F_{\mathrm{pressure}} \approx 6P$. לכן תאוצת החללית חייבת להיות קטנה מ-$5g$. קל להיווכח שזה נכון כי מהאי-שוויון $m(g+a)\leq 6mg$ נובע $a\leq 5g$.

אם החללית נעה במסלול מעגלי סביב כדור הארץ (המנועים שלה כבויים והיא נופלת חופשית), הרי שתאוצתה שווה לתאוצת הנפילה החופשית $\mathbf{a}=\mathbf{g}$. מהדוגמה של המעלית אנו יודעים כי זה אומר ש-$Q=0$. כלומר האסטרונאוט לא לוחץ על המשטח, והוא ירגיש כאילו הוא “איבד את משקלו”.

לפיכך אפשר לומר כי

מצב חוסר משקל מתקיים כאשר מערכת לא אינרציאלית (במקרה שלנו – החללית) נעה ביחס לכדור הארץ בתאוצה $\mathbf{a}=\mathbf{g}$.

יש לציין כי ערך זה של התאוצה לא אומר שום דבר על אופי מסלול התנועה. התנועה יכולה להיות בקו ישר, אם במקרה של המראה או נחיתה אנכית המנועים יהיו כבויים, או במסלול עקום, אם החללית נעה סביב כדור הארץ – כאן התאוצה הינה צנטריפטלית. על מנת להגיע למצב של חוסר משקל, כלל לא משנה באיזה מסלול לנוע, העיקר שהעצם נע בתאוצה השווה לתאוצת הנפילה החופשית.