אחד ההישגים החשובים ביותר של הפיזיקה המודרנית הוא גילוי התכונות המיוחדות של הליום נוזלי. התכונות הללו בלתי צפויות ואף נראות פרדוקסליות. כיום מכלול התכונות הללו נקרא בשם נוזלות-על (superfluidity) – תופעה אותה גילה פיזיקאי סובייטי פיוטר קפיצה בשנת 1938. כמובן שנוזלות-על איננה רק העובדה שהליום נוזלי זורם יותר טוב מכל נוזל אחר. כפי שהראה הפיזיקאי הסובייטי לב לנדאו בשנת 1941 בעבודתו אודות נוזלות-על של הליום-4, תכונות הליום על-נוזלי הן תכונות האופייניות לכל החומרים בטמפרטורות מספיק נמוכות, רק שאצל הליום התכונות הללו יותר בולטות. זאת בעצם הסיבה לכך שחקר ההליום הנוזלי השפיע מאוד על תחומים רבים אחרים בפיזיקה.

תכונות ההליום העל-נוזלי

לא במקרה אומרים שהליום הינו גז אינרטי. האינטראקציה של האטומים שלו עם אטומים של יסודות אחרים ועם עצמם היא חלשה ביותר. זאת גם הסיבה לכך שהליום עובר ממצב גזי למצב נוזלי בטמפרטורה נמוכה מאוד ($4.2 \text{K}$ או $-268.9^{\circ} \text{C}$ בלחץ אטמוספרי רגיל). הליום לא מתמצק גם בטמפרטורות יותר נמוכות. הליום מוצק קיים רק בלחצים גבוהים (כ-25 אטמוספרות, בטמפרטורות הקרובות לאפס המוחלט), כאשר בגלל קרבתם, האטומים מצליחים להתלכד וליצור קשרים.
בטווח הטמפרטורות שבין $4.2 \text{K}$ ל-$2.2 \text{K}$ הליום נוזלי מתנהג מכל הבחינות כמו כל נוזל רגיל אחר. בטמפרטורה של $2.2 \text{K}$ מתרחש מעבר של הליום ממצב רגיל, הנקרא גם הליום-I, למצב מיוחד – הליום-II, המאופיין על-ידי נוזלות-על. אנו ניווכח כי תוצאות הניסויים עם הליום-II שנציג בהמשך לא עולות בקנה אחד עם מה שאנו רגילים אליו בנוזלים אחרים, ונראה כי על מנת להסבירם נצטרך להכיר מספר מושגים חדשים.

 צמיגות ונוזלות-על

התעלומה הראשונה מתגלה כאשר מודדים צמיגות (כלומר, חיכוך פנימי) של הליום-II. בנוזלים רגילים הצמיגות (או יותר נכון, מקדם הצמיגות) יכולה להימדד בשני דרכים. דרך אחת היא להכניס את הנוזל אל תוך מיכל בעל פתח צר מלמטה ולמדוד את מהירות הנזילה דרך הפתח בהשפעת הכבידה (איור 1).

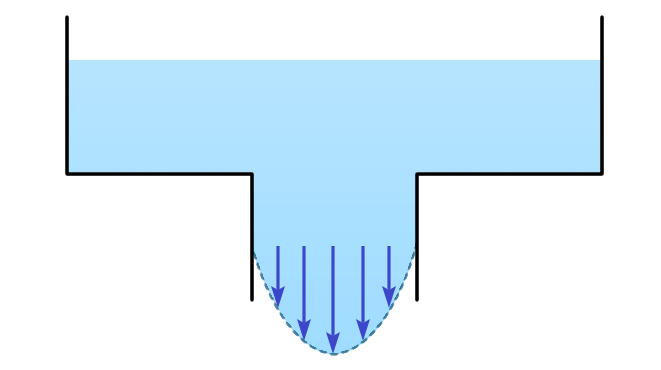
איור 1 – נזילה דרך פתח של מיכל

מהירות הנוזל אשר מתוארת על ידי החצים הינה מקסימלית בחלק האמצעי של הפתח והיא קטנה ככל שמתקרבים אל הדפנות. לפיכך, שכבות שונות של נוזל נעות במהירויות שונות, ולכן נוצר ביניהן כוח חיכוך פנימי שמשפיע על מהירות הדליפה של הנוזל. גודל המהירות הזאת קובע את צמיגות הנוזל.
הדרך השנייה (איור 2) היא מדידה של זמן ריסון התנודות הסיבוביות של דיסקית השקועה בנוזל. כתוצאה מתנועתה הדיסקית סוחבת אחריה את הנוזל אשר נמצא בקרבתה, בעוד שהנוזל המרוחק ממנה כמעט ולא מושפע מסיבובה ונמצא במנוחה. כמו קודם, נוצר מצב שבו שכבות שונות של נוזל נעות במהירויות שונות ונוצר ביניהן חיכוך. כתוצאה מכך, אנרגיית התנודות בהדרגה הופכת לאנרגיית חום. את צמיגות הנוזל אפשר למדוד במקרה זה באמצעות זמן הריסון (כלומר הזמן שיעבור עד שהדיסקית תפסיק להסתובב – כל האנרגיה המכנית שלה תעבור לאנרגיית חום כתוצאה מהחיכוך).

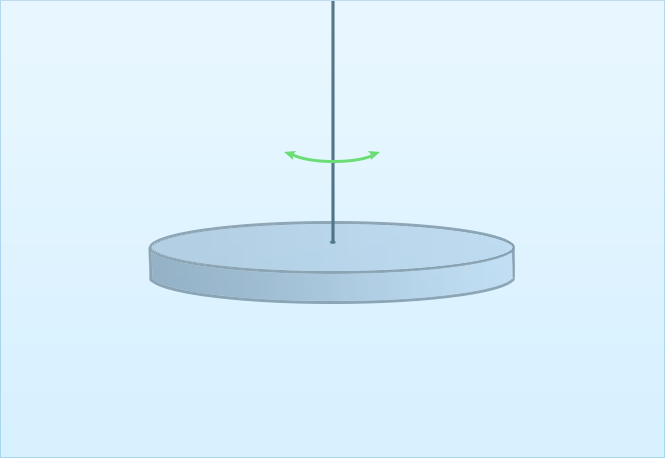
איור 2 – דיסקית טבולה בתוך נוזל ומבצעת תנודות סיבוביות

ניסויים עם הליום נוזלי אשר בוצעו בדרך הראשונה, הראו דבר מעניין: כל עוד ההליום נמצא במצב רגיל, ערכי הצמיגות בולטים וניתנים למדידה. אולם לאחר המעבר להליום-II, הצמיגות נופלת בפתאומיות לערכים אפסיים. כשלעצמו, זה אולי לא מפתיע במיוחד. יכול להיות שהליום-II הוא בסך הכול נוזל רגיל בעל צמיגות מאוד נמוכה? אז זהו שלא ממש. כאשר ביצעו ניסויים בדרך השנייה, קיבלו שהצמיגות של הליום-II היא מאותו סדר גודל כמו של הליום-I. נוצרת כאן סיטואציה די פרדוקסלית – הליום-II, להבדיל מנוזלים רגילים, מתגלה כצמיג בניסוי אחד וכלא צמיג בניסוי אחר.

התכונה הבסיסית של הליום לנזול דרך חריצים צרים ללא כל צמיגות נקראת נוזלות-על.

העברת חום ותנועה

בנוזלים רגילים קיימים שני מנגנונים להעברת חום – הולכת חום וקונווקציה. הולכת חום בנוזלים נייחים הינה העברת חום ממקומות בעלי טמפרטורה גבוהה למקומות בעלי טמפרטורה נמוכה. נראה זאת בדוגמה הבאה (איור 3).

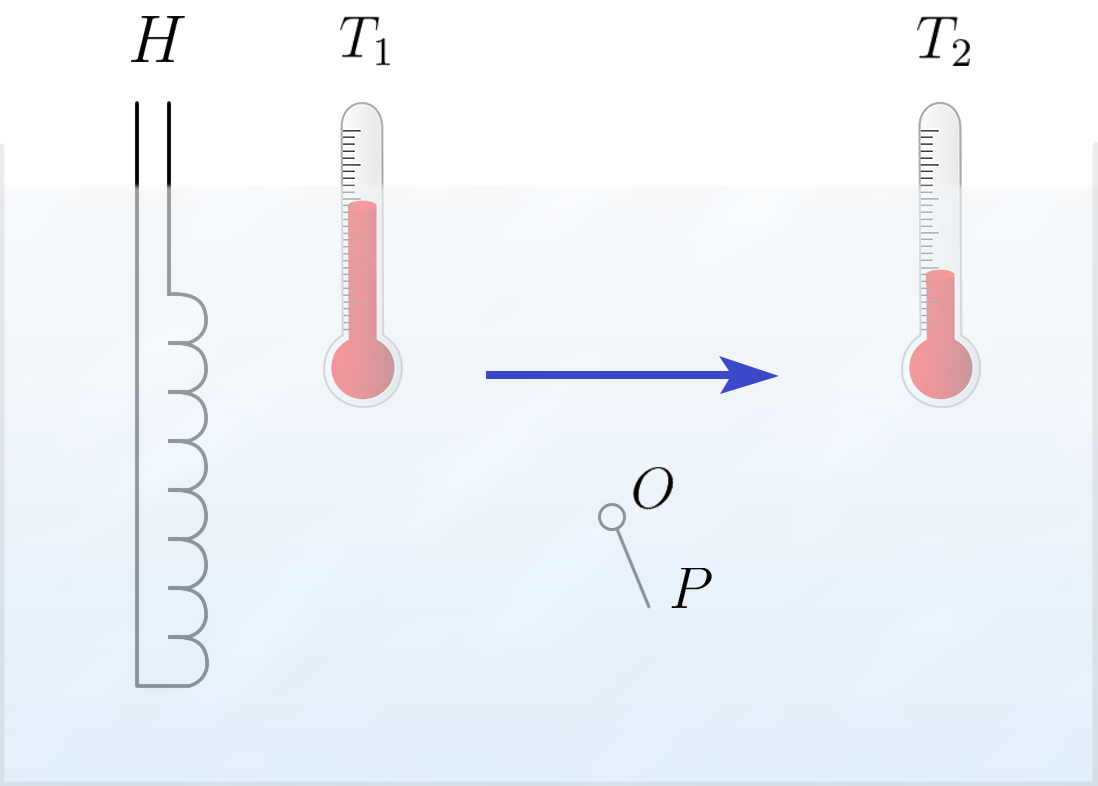
איור 3 – מעבר חום מתרחש כתוצאה מהפרש טמפרטורות. אם העלה $OP$ פונה לכיוון מסוים, אז יש גם מעבר של נוזל

מחמם $H$ פולט חום בכיוון המצוין על ידי החץ: טמפרטורת הנוזל קטנה משמאל לימין. אם העברת חום מתרחשת באמצעות הולכת חום, הנוזל הינו נייח, ועובר בו שטף של חום (כמות החום המועברת בחומר ליחידת זמן בניצב לפני יחידת שטח) ממקומות חמים למקומות קרים יותר. כמות החום העוברת ליחידת זמן שונה מאפס כאשר מד הטמפרטורה $T_1$ מורה על ערך יותר גבוה ממד הטמפרטורה $T_2$. זה דומה לזרימת זרם חשמלי, כאשר פוטנציאל בנקודה מסוימת גבוה מפוטנציאל בנקודה אחרת. מבחינה כמותית ניתן לתאר את הולכת החום על ידי מקדם שהינו היחס שבין שטף החום להפרש הטמפרטורות. מקדם כזה נקרא מקדם מוליכות חום. ככל שמוליכות החום בנוזל גבוהה יותר, כך יותר חום עובר מאזור אחד לאזור אחר בהינתן הפרש טמפרטורות קבוע. כלומר צריך הפרש טמפרטורות קטן יותר בכדי לקבל את אותו השטף.

מעבר חום בדרך של קונווקציה קשור לתנועה של הנוזל עצמו. אם בגלל סיבה כזאת או אחרת הנוזל מתחיל לנוע משמאל לימין, יתרחש מעבר של חום בכיוון זה, מפני שלנוזל יש אנרגיית חום מסוימת. במקרה זה מעבר החום איננו תוצר של הפרש טמפרטורות אלא תוצר של תנועה מכנית של הנוזל עצמו. אם כן, מעבר חום בדרך של קונווקציה יכול להתרחש גם אם הוריית מד הטמפרטורה $T_1$ שווה לזו של $T_2$.

כאשר בנוזלים רגילים מתרחשת קונווקציה, שטף החום הוא די ניכר. אם השטף קטן, הרי שמדובר בהולכת חום ולא בקונווקציה, ולכן אנו רשאים לקבוע את מקדם מוליכות החום של הנוזל על ידי מדידה של כמות החום העוברת בו ליחידת זמן ועל ידי מדידה של הפרש הטמפרטורות. אם נבצע ניסוי עם הליום-II אנו ניווכח כי כמויות מזעריות של חום עוברות דרך הנוזל כאשר $T_1=T_2$. ניתן להסיק מכך שתי מסקנות. ראשית, אם נניח שבמקרה של הליום-II יש לנו עסק עם הולכת חום ולא עם קונווקציה, נצטרך לקבוע כי מוליכות החום של הליום-II היא אינסופית. אולם אפשר להניח כי בהליום-II החום מועבר בתהליך של קונווקציה, ואז אין כל צורך בהפרש טמפרטורות.

על מנת לקבוע מה באמת קורה, נבצע ניסוי אחר. נשים בהליום עלה $P$ אשר יהיה חופשי להסתובב סביב ציר $O$ (איור 3 מקודם). אנו נגלה כי תמיד כאשר עובר שטף של חום בהליום-II העלה נוטה לכיוון השטף, מה שמעיד על תנועת הנוזל. לפיכך, אומתה ההשערה השנייה שלנו.
אולם לא הכל כל כך פשוט. הניסוי המתואר באיור 4 בוצע על ידי פיוטר קפיצה בשנת 1941. מחמם $H$ נמצא בתוך מיכל הממולא באופן חלקי בהליום-II. למיכל יש פתח יחיד בצד והוא נמצא בתוך אמבט מלא בהליום-II. בקרבת הפתח מוצב אותו עלה $P$ על ציר $O$ כמו בניסוי הקודם. אם נפעיל את המחמם, שטף החום ידלוף מהמיכל החוצה דרך הפתח. גם כאן העלה סוטה ימינה מה שמראה כי השטף יוצא מהמיכל דרך הפתח. אבל מעבר לזה, קורה כאן דבר מדהים –  רמת הנוזל בתוך המיכל לא יורדת. גם אם נחכה הרבה מאוד זמן, העלה עדיין יהיה מופנה ימינה. לכאורה, הנוזל דולף מהמיכל, אולם רמת הנוזל במיכל לא משתנה. זה מוכיח את העובדה שחוקי התנועה של הליום-II שונים מחוקי תנועה של נוזלים רגילים –  תהליך הקונווקציה בהליום-II הינו מיוחד במינו.

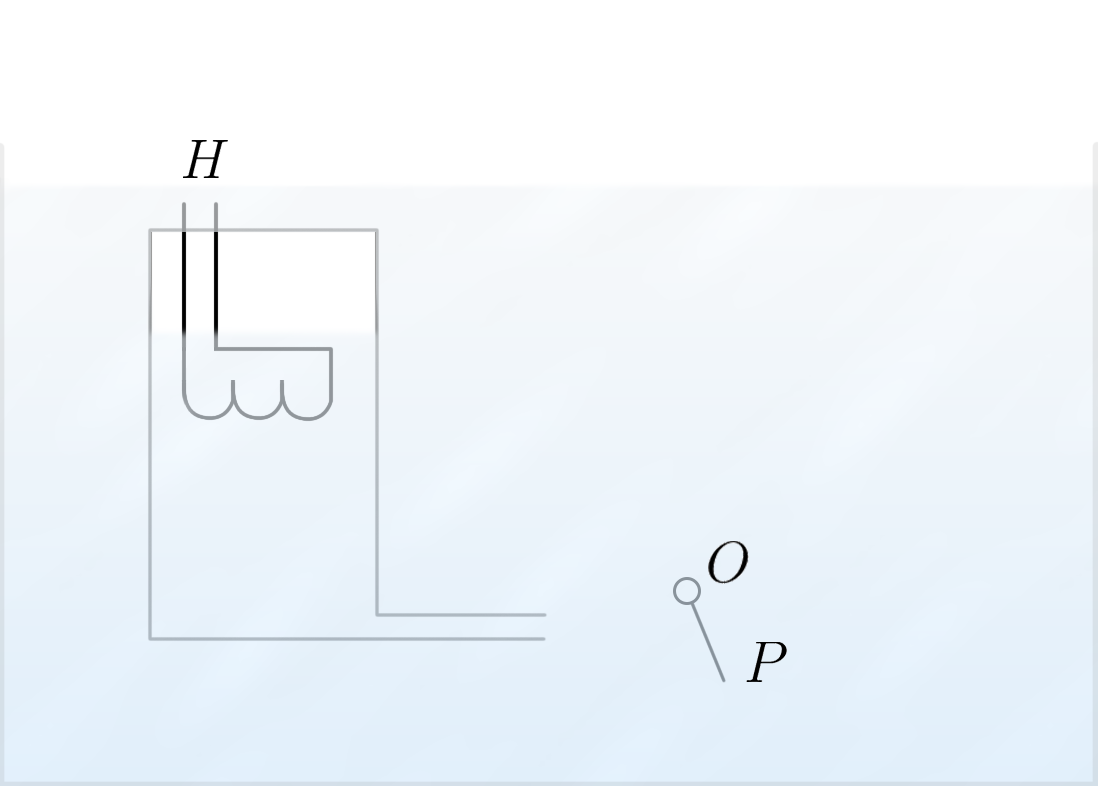
איור 4 – רמת ההליום בכלי לא יורדת, אף על פי שהעלה מוטה

תורת נוזלות-העל

בטמפרטורות החדר מתקיימים גופים מוצקים, נוזלים וגזים. אם מעלים את הטמפרטורה כל הגופים המוצקים והנוזלים הופכים לגז, כלומר למערכת המורכבת ממולקולות נפרדות הנעות בצורה חופשית. אם ממשיכים להעלות את הטמפרטורה, תנועת האטמים המרכיבים את המולקולות הופכת להיות כה אינטנסיבית שהמולקולות מתפרקות. בטמפרטורות אף יותר גבוהות (מסדר גודל של עשרת אלפים מעלות) האלקטרונים משתחררים מן האטומים החופשיים. כל חומר בטמפרטורות כאלה הוא בעצם גז המורכב מאלקטרונים וגרעינים חופשיים – זהו מצב הנקרא פלזמה.
הליום-II זהו נוזל המסוגל להתקיים רק בטמפרטורות מספיק נמוכות (מ-$2.2^{\circ} \text{K}$ ומטה). לכן בכדי להסביר את תכונותיו, נצטרך קודם להבין כיצד באופן כללי מתנהגים חומרים בטמפרטורות נמוכות.

עירור אלמנטרי

נראה עתה מה קורה כאשר מתבצע התהליך ההפוך, כלומר כאשר מקררים מערכת. תחילה, במקרה של פלזמה, האלקטרונים והגרעינים נעים באופן חופשי. עם הורדת הטמפרטורה, האלקטרונים והגרעינים מתאחדים לאטומים ואז רק האטומים עצמם יכולים לנוע חופשית. אומרים במקרה כזה שמספר דרגות החופש של המערכת ירד – המערכת הפכה להיות פחות חופשית, שכן האלקטרונים נקשרו לגרעינים. ניתן לומר שעם הורדת הטמפרטורה יש פחות סוגים אפשריים של תנועת חום. אם נמשיך להוריד את הטמפרטורה, נראה כי מספר דרגות החופש של המערכת יקטן עוד יותר. תנועת החום של אטומים יחסית למרכז הכובד של המולקולה שהם מרכיבים תיפסק. בטמפרטורת החדר ובטמפרטורות נמוכות יותר אפשר בכלל לשכוח מהעובדה שמולקולות מורכבות מאטמים, ושהאטומים מורכבים מאלקטרונים ומגרעינים – תנועת החום של המולקולות היא תנועה של שלם. כאשר גז או נוזל הופכים למוצק, המולקולות לא יכולות לנוע בצורה חופשית למרחקים גדולים והן רק מבצעות תנודות קטנות סביב מצבי שיווי משקל מסוימים.
כמובן שתהליך “איבוד” דרגות החופש ממשיך גם בטמפרטורות הנמוכות מטמפרטורת החדר. מפני שבאפס המוחלט כל תנועות חום חייבות להיפסק, אפשר להניח כי בטמפרטורות מאוד נמוכות, בכל חומר, מתקיים סוג אחד בלבד של תנועת חום אשר מצליח “לשרוד” בטמפרטורות כאלה. לסוג זה של תנועת חום קוראים עירור אלמנטרי. עירורים אלמנטריים משתנים מחומר לחומר. להבנת העירורים האלמנטריים חשיבות רבה בחקר החומר בטמפרטורות נמוכות.

מה הם העירורים האלמנטריים בהליום-II? כמובן שזו לא תנועה של אטומים בודדים, שכן זוהי תפישה קלאסית וכפי שראינו קודם, החוקים הקלאסיים אינם ישימים במקרה של הליום-II. לב לנדאו הניח כי עירור אלמנטרי בהליום-II זה למעשה תנועה קולקטיבית של אטומים, כלומר תנודות קול, ולא תנועה של אטומים בודדים. הוא הראה כי מהנחת היסוד הזאת אפשר לפתח תאוריה שלמה שתוכל להסביר את תופעות הנוזלות-על של הליום. הנחה זו של לנדאו אומתה על ידי ניסויים רבים.

קיימים שיקולים פשוטים המאפשרים להגיע למסקנה שאליה הגיע לנדאו. בחומרים רגילים, ירידה במספר סוגי תנועות חום של מולקולות בודדות בא לידי ביטוי בהתמצקות הנוזל. כאמור, בגוף מוצק המולקולות מסוגלות לבצע רק תנודות קטנות סביב מצבי שיווי משקל מסוימים. אולם אין אלה תנודות חופשיות של חלקיקים בודדים. תנודות של מולקולה אחת ישר מועברות למולקולה סמוכה וכתוצאה משרשרת התנודות הזאת אנו מקבלים תנודות קולקטיביות של כלל המולקולות – אלו הם למעשה גלי קול. גלי קול יכולים לנוע בכל הנוזלים, אך בנוזלים רגילים הם תמיד בסופו של דבר נחלשים כי האנרגיה שלהם הופכת לאנרגיית חום של חלקיקים בודדים. כפי שכבר ראינו, בהליום-II תנועות חום כאלה לא יכולות להתקיים ולכן האופציה היחידה שנשארת זה תנודות קול. תהליך המעבר מתנודות אינדיבידואליות לתנודות קולקטיביות חייב במוקדם או במאוחר לקרות בכל חומר, רק שבהליום-II זה מתרחש כאשר הוא נמצא במצב נוזלי מפני שהאינטראקציה החלשה שבין האטומים שלו לא מאפשרת לו להתמצק.
תכונה זו של הליום נוזלי מבדילה אותו מכל הנוזלים האחרים והיא האחראית לכל התופעות המוזרות שאותן הזכרנו בהתחלה. ההשערה שהעירורים האלמנטריים בהליום-II הם למעשה תנודות קול מובילה אותנו למסקנה שכל האנרגיה הפנימית של התנודות היא אנרגיה של גלי קול. עם עלייה בטמפרטורה, האנרגיה הפנימית גדלה ולכן אנרגיית גלי הקול גם היא צריכה לגדול.

תכונות שונות של גלי קול בנוזלים

1. התפשטות גלי הקול מלווה בהעברת נוזל בכיוון ההתפשטות. אם נעקוב אחר תנועת חלקיק מסוים בנוזל בו מתפשטים גלי קול, נגלה כי מלבד התנודות הרגילות שהוא מבצע הוא גם נע בצורה איטית בכיוון התפשטות הגל.
   אם במערכת חלקיקים כלשהי מתרחש מעבר מסה ממקום למקום זה אומר שלמערכת יש תנע מסוים השונה מאפס. כלומר גם גל הקול נושא תנע מסוים בכיוון התפשטותו. זה אומת ע”י ניסויים רבים. לדוגמה, אם גל הקול פוגע בקיר ומוחזר ממנו או נבלע בו, השינוי בתנע שלו מועבר לקיר ונוצר מה שנקרא לחץ קול.
   בהליום-II בדרך כלל אנרגיית גלי הקול המתפשטים בכיוונים שונים שווה ולכן אין העברת נוזל. אך אם מסיבה כלשהי גלי הקול מקבלים כיוון התפשטות מועדף, בכיוון זה יתרחש מעבר נוזל. זה מזכיר את מצב הענן האלקטרוני במוליך – כשאין מתח האלקטרונים נעים בצורה כאוטית כך שבממוצע לא מתרחש מעבר מטען, אך אם מפעילים מתח, הענן האלקטרוני יתחיל לנוע בכיוון מסוים שכן האלקטרונים יאיצו אל עבר הפוטנציאל החיובי.
2. על מנת שעצם הטבול בתוך נוזל יצור גלי קול צריך שהוא יבצע תנודות. אם העצם נע בתוך הנוזל במהירות קבועה ולא מבצע שום תנודות (למשל ע”י שינוי צורתו, גודלו וכו’) הוא לא יכול לפלוט גלי קול. הטענה הזאת נכונה כל עוד מהירות הגוף לא גדולה ממהירות הקול, שכן במהירויות על-קוליות הגוף יכול לפלוט גלי קול גם אם הוא לא מאיץ ולא מבצע שום תנודות, רק מעצם היותו נע במהירות על-קולית קבועה.
   כמובן שכל זה נכון גם אם העצם נמצא במנוחה והנוזל נע סביבו – כלומר אם הנוזל זורם סביב הגוף במהירות הנמוכה ממהירות הקול, לא תתרחש פליטת גלי קול.

הסבר תכונות הליום-II

ניתן להסביר את התופעות שראינו בהליום-II על סמך תכונות גלי קול בנוזלים. כאשר נוזל רגיל זורם דרך פתח כלשהו נוצר חיכוך – האנרגיה הקינטית של הנוזל הופכת לאנרגיית חום כתוצאה מאינטראקציה של חלקיקי הנוזל עם החספוסים של הדפנות. היינו מצפים שבמקרה של הליום-II, שבו האנרגיה הפנימית היא אנרגיית גלי הקול, הגדלת האנרגיה הפנימית כתוצאה מהחיכוך הייתה גורמת לעלייה באנרגיית גלי הקול ולכן ההליום היה פולט גלי קול בזרימתו דרך הפתח. אך כפי שראינו, פליטת גלי קול לא יכולה להתרחש במהירויות נמוכות. זה שהליום-II לא יכול לפלוט גלי קול אומר למעשה שלא יכולים להיווצר בו גלי קול חדשים. אולם כפי שכבר נוכחנו לדעת, בהליום-II כבר יש גלי קול כתוצאה מהעירורים האלמנטריים. על מנת להבין את האינטראקציה שלהם עם דפנות הכלי שדרכו זורם הליום-II נעבור למערכת ייחוס הצמודה לנוזל עצמו, כלומר נניח כי לא הנוזל עצמו נע אלא הדפנות נעות בכיוון הנגדי. הדפנות לא סוחפות את הנוזל אך הן כן סוחפות את גלי הקול, כי כאשר גלי הקול בהליום-II מתנגשים בדפנות הם מקבלים מהם תנע מסוים בכיוון תנועתם. זאת אומרת שתנועת הדפנות נותנת לגלי הקול כיוון התפשטות מועדף. מכאן שמתרחשת העברת נוזל בכיוון הנ”ל. כלומר הדפנות סוחפות חלק קטן מהנוזל עצמו.

אפשר לתאר את הליום-II כתרכובת של שני נוזלים המסוגלים לנוע באופן חופשי ובלתי תלוי זה מזה. תנועה של נוזל אחד לא מלוות בחיכוך ולכן זהו המרכיב העל-נוזלי. הנוזל האחר מתנהג כמו נוזל רגיל שמתחכך עם הדפנות והוא נקרא המרכיב הנורמלי. סך המסה של שני המרכיבים היא מסת הנוזל כולו. כמובן שזהו תיאור קונבנציונלי בלבד, כי כל אטומי הליום משתתפים בשתי התנועות יחד ולא ניתן לומר שקבוצה אחת של אטומים עושה משהו אחד וקבוצה אחרת עושה משהו אחר.
עם עלייה בטמפרטורה אנרגיית גלי הקול גדלה ומסת המרכיב הנורמלי גם היא גדלה. בטמפרטורה מסוימת נוצר מצב שבו מסת המרכיב הנורמלי שווה למסת כל הנוזל והתנועה העל-נוזלית נפסקת, שכן המרכיב העל-נוזלי נעלם – כך הליום-II עובר להליום-I, אשר מתנהג ככל נוזל רגיל אחר.
אם גוף כלשהו נע בהליום-II במהירות קבועה הנמוכה ממהירות הקול, הוא לא נתקל בשום חיכוך שכן עצם קיום החיכוך היה מצריך ביצוע עבודה נגדו, כלומר הייתה מתבזבזת אנרגיה שהייתה הופכת לאנרגיית חום ולכן היו נפלטים גלי קול. אולם כפי שכבר אמרנו, פליטת גלי קול איננה אפשרית במקרה זה, לכן אין חיכוך. אפשר לומר, אם כן, שלא מופעל לחץ על גוף אשר זורם בסביבה על-נוזלית. אולם במקרה של נוזל נורמלי כן יהיה לחץ מפני שגלי הקול יתנגשו בעצם ויקנו לו תנע מסוים.

עכשיו, אחרי שרכשנו מספיק ידע תיאורטי, נוכל להסביר את תוצאות הניסויים. בניסוי הראשון (נזילה דרך פתח) ראינו כי להליום-II אין צמיגות. זה נובע מכך שהמרכיב העל-נוזלי של הליום יוצא מהר מהפתח ללא חיכוך – דבר שלא יכול לקרות עם נוזל רגיל שיזרום הרבה יותר לאט דרך הפתח.
בניסוי עם הדיסקית נמדדה צמיגות שונה מאפס מפני שהדיסקית נעה בתוך נוזל המורכב משני נוזלים. ריסון תנודותיו מתרחש כתוצאה מהאינטראקציה שלו עם הנוזל הנורמלי. כלומר בניסוי הראשון בא לידי ביטוי המרכיב העל-נוזלי של הליום-II בעוד שבניסוי השני – המרכיב הנורמלי.

קרינת חום בהליום-II הוא למעשה תהליך של פליטת גלי קול. מעבר חום בכיוון מסוים מתרחש מפני שאנרגיית גלי הקול המתפשטים בכיוון זה גדולה מאשר בכיוונים אחרים. לפיכך הכיוון בו מועבר חום זה גם הכיוון “המועדף” על גלי קול ועל המרכיב הנורמלי. מכאן שהתהליך של מעבר חום בהליום-II תמיד מלווה בתנועה של הנוזל הנורמלי, כלומר מדובר במנגנון קונווקציה. זאת הסיבה לכך שבניסוי המתואר באיור 3 הוריית מדי הטמפרטורה הייתה שווה והעלה סטה בכיוון שטף החום.

אם מעבר החום מתרחש בהליום-II שנמצא בתוך כלי סגור כמו באיור 4, הנוזל לא זורם לאף כיוון מפני שהפרש הלחצים הנוצר בגלל מעבר חום גורם למרכיב העל-נוזלי של הליום לזרום בכיוון ההפוך. יותר מזה, מהירות המרכיב העל-נוזלי היא כזאת, שבסך הכול, לא מתרחש מעבר מסה ולכן גם רמת הנוזל לא משתנה. הסטייה של העלה מעידה על כך שמתוך הכלי זורם המרכיב הנורמלי, בעוד שהמרכיב העל-נוזלי נשאר בלתי נראה, שכן הוא לא מפעיל לחץ על הגופים שסביבם הוא זורם.