
מודל האטום ומכניקת הקוונטים
בבית הספר בוודאי למדתם על מבנה האטום ועל המודלים שבנו לו מדענים שונים לפי הסדר הכרונולוגי. בהתחלה הכרנו את המודל של תומסון, לפיו האטום הוא כמו עוגת צימוקים – המטען החיובי מפוזר בתוכו בצורה אחידה והאלקטרונים שנושאים מטען שלילי משובצים בו במנוחה – כמו צימוקים על פני עוגה. אבל אז נוכחנו לדעת שהמודל לא טעים כמו שהוא נראה, מפני שהוא לא יכל להסביר את ספקטרום הפליטה של אטום מימן שכלל אינסוף קווים ספקטרלים וגם כי הניסוי של רתרפורד הראה שהאטום בנוי בצורה שונה. לאחר מכן ראינו את הניסוי של רתרפורד שבו הוא שלח אלומה של חלקיקי אלפא הטעונים חיובית אל עבר פיסה דקה של נייר זהב וגילינו שמרבית החלקיקים הצליחו לעבור דרכה ללא סטייה משמעותית, אך היו כמה שסטו בצורה חדה. בהתחלה חשבנו שזאת סתם טעות, כי אולי החלקיקים הללו מלכתחילה לא נעו ישר, אבל הסתבר שזאת לא טעות. רתרפורד הציע מודל שונה שלפיו כל המטען החיובי מרוכז בגרעין קטן מאוד והאלקטרונים נעים סביבו בתנועה מעגלית. המודל הזה הסביר בצורה נפלאה את תוצאות הניסויים, כי אותם החלקיקים שעברו בקרבת הגרעין הרגישו כוחות דחייה חזקים בעוד שהחלקיקים האחרים שהיו רחוקים מהגרעין לא הרגישו כוחות חזקים מדי (וזאת בגלל האופי של חוק קולון – $F \propto \frac{1}{r^2}$). אבל אז שוב נאלצנו לחפש מודל אחר, שכן לפי המודל של רתרפורד האלקטרון כל הזמן צריך לפלוט קרינה אלקטרומגנטית (כי תנועה מעגלית קצובה זאת תנועה מואצת), לאבד אנרגיה ובסופו של דבר לפול על הגרעין – כמובן שזה לא קורה, אחרת לא היינו עכשיו בחיים. פה הכרנו את המודל של בוהר – סלט מוזר של מכניקה קלאסית, רעיונות דה-ברויי ומכניקת הקוונטים (כמובן שאז היא עוד לא הייתה קיימת) שהצליח להסביר את ספקטרום הפליטה והבליעה של אטום המימן. באותה התקופה (שנת 1913) זה היה הישג ענק – לפתע הגיעה ההבנה שבטבע לא רק לאנרגיה של האור יש אופי בדיד אלא גם לרמות האנרגיה באטום ערכים דיסקרטיים. למרות ההצלחה, היו דברים בעייתיים במודל שלו – מצד אחד מדברים על אלקטרון כעל חלקיק לכל דבר שנע בתנועה מעגלית במסלולים מותרים ומצד אחר מסבירים את המסלולים המותרים באמצעות גלי דה-ברויי – אז תחלטיו כבר, חלקיקים קלאסיים או גלים? ואם זה לא היה מספיק, המודל של בוהר לא עבד בכלל באטומים של יסודות אחרים שאינם מימן כמו למשל הליום (שהיה בעל שני אלקטרונים בלבד). בכל מקרה, זה עדיין היה ניסיון נועז וחשוב שאיפשר מאוחר יותר לפתח מודל מוצלח של האטום. למעשה, בוהר הבין שבכדי להסביר מה קורה באטום צריך להתחשב איכשהו גם במאפיינים הגליים של החלקיקים. הבעיה העקרונית במודל שלו הייתה, כאמור, הסתירה העצמית כתוצאה משילוב של שתי תורות שונות לגמרי. בשלב זה היה צורך במודל חדש שיהיה עקבי – או שיתבסס כולו על הרעיונות הניוטוניים הקלאסיים או שיתבסס כולו על רעיונות קוונטיים.
כאן לתמונה נכנסת מכניקת הקוונטים – תאוריה גלית טהורה שהצליחה להסביר את כל מה שהמודל של בוהר נכשל בו ואף יותר. יתר על כן, מסתבר כי עובדה חשובה כמו קוונטיזציה של רמות אנרגיה שהייתה למעשה הנחת היסוד במודל של בוהר, נובעת באופן טבעי מהמשוואה המרכזית במכניקת הקוונטים – משוואת שרדינגר.
פונקציית גל
כידוע, לחלקיקים חומריים יש תכונות גליות. אך כיצד ניתן לפרש את גלי דה-ברויי? איזה מן גלים מתארים את התנהגותם של חלקיקים מיקרוסקופיים כמו למשל אלקטרון? מקס בורן טען שאלו גלי הסתברות: ריבוע האמפליטודה של גל דה-ברויי בנקודה כלשהי מייצג את מידת ההסתברות של מציאת החלקיק באותה הנקודה. נדגיש כי אין קשר בין גלי דה-ברויי לבין שדה אלקטרומגנטי כלשהו או גל אלקטרומגנטי.
במכניקה קלאסית יכולנו לנבא את תנועת החלקיק או הגוף באמצעות החוק השני של ניוטון. תנאי ההתחלה – מהירות ומיקום של חלקיק בנקודה מסוימת במרחב בזמן $t=0$ היוו תיאור מלא של מצב החלקיק.
מניסויים שבהם התגלו התכונות הגליות של חלקיקים ומהמשמעות של גלי דה-ברויי אפשר להיווכח כי במכניקת הקוונטים תנאי ההתחלה שמתארים את מצב החלקיק באופן המלא ביותר צריכים להיות שונים. הרי אנחנו יכולים לדבר רק על ההסתברות של מציאת חלקיק בזמן נתון ובנקודה נתונה, או יותר נכון, בנפח אינפיניטסימלי $\Delta V$. אם כן, ההבדל בין תנאי ההתחלה במכניקה קלאסית לבין תנאי ההתחלה במכניקת הקוונטים מתבטא בכך שבמכניקת הקוונטים התיאור המלא ביותר של חלקיק ניתן על ידי הסתברות של מציאתו בנפח מזערי מסוים $\Delta V$ בזמן מסוים $t$. כאמור, ההסתברות הזאת פרופורציונית לריבוע האמפליטודה של גל דה-ברויי.
לכן במכניקת הקוונטים רושמים פונקציה מסוימת $\Psi (x,y,z,t)$ שהיא פונקציה של ארבעה משתנים – שלוש קואורדינטות $x, y, z$ וזמן $t$. הפונקציה הזאת נקראת פונקציית גל. לפונקציה כשלעצמה אין משמעות פיזיקלית, אולם בוחרים אותה כך שההסתברות $P$ למציאת חלקיק בנפח אינפיניטסימלי $\Delta V$ יהיה פרופורציוני ל-$\left|\Psi\right|^2$ ולנפח $\Delta V$:
\[P=|\Psi|^2 \Delta V\]לפי הנוסחה הזאת אפשר לראות כי רק לריבוע הערך המוחלט של הפונקציה $\Psi$ יש משמעות:
\[|\Psi|^2=\frac{P}{\Delta V}\]הגודל $\left|\Psi\right|^2$ נקרא צפיפות ההסתברות. חשוב להבין שזאת לא ההסתברות עצמה (שהיא $P$). צפיפות ההסתברות מראה כיצד ההסתברות למציאת חלקיק מפוזרת במרחב. במילים אחרות, הגודל $\left|\Psi\right|^2$ קובע את עוצמת גלי דה-ברויי.
(הערה: בהמשך נשתמש ב-$\Psi$ גם לסימון פונקציית גל ללא תלות בזמן)
מה שחדש כאן זה האופי של הגל – זהו גל הסתברותי. באמצעות פונקציית הגל במכניקת הקוונטים מגדירים מצב של מערכת. היא מהווה פתרון למשוואה שהזכרנו קודם – משוואת שרדינגר. את המשוואה פיתח הפיזיקאי האוסטרי ארווין שרדינגר בשנת 1926. מבחינת חשיבותה במכניקת הקוונטים, משוואת שרדינגר דומה לחוק השני של ניוטון במכניקה ניוטונית. כמו שבמכניקה ניוטונית אנחנו יכולים לפתור בעזרת החוק השני של ניוטון כל בעיית תנועה של גופים מאקרוסקופיים כך גם במכניקת הקוונטים אפשר לפתור בעיות תנועה של גופים מיקרוסקופיים באמצעות משוואת שרדינגר.
למשוואת שרדינגר ערך פרקטי רב, שכן היא מאפשרת לתאר תנועה של אלקטרונים באטומים, מולקולות וגבישים של חומרים מוצקים. באמצעות המשוואה הזאת ניתן להוכיח את העובדה שאנרגיות האלקטרונים באטומים, במולקולות ובגבישים הינן בדידות. משוואת שרדינגר לא ניתנת להוכחה כשם שהחוק השני של ניוטון לא ניתן להוכחה. נכונות משוואת שרדינגר נובעת מכך שכל המסקנות שאנחנו יכולים להסיק ממנה תואמות את העובדות הניסיוניות. נציג מקרה פרטי של המשוואה כשהחלקיק נע במימד אחד לאורך ישר אחד $x$:
כאשר $E$ – האנרגיה הכוללת של החלקיק, $U=U(x)$ – האנרגיה הפוטנציאלית של המערכת. זוהי משוואה דיפרנציאלית שבאמצעותה ניתן למצוא את הביטוי ל-$\Psi$ ולפיכך גם לגלות את ההסתברות למציאת חלקיק באזור מסוים במרחב.
מכל האמור לעיל נובע כי למכניקת הקוונטים אופי סטטיסטי. לא ניתן לקבוע מיקום של חלקיק במרחב וגם לא את מסלול תנועתו. בעזרת פונקציית הגל ניתן רק לנבא את ההסתברות של מציאת חלקיק בנקודה כזאת או אחרת במרחב.
במבט ראשון אפשר לחשוב שמכניקת הקוונטים נותנת מידע פחות מדויק מאשר המכניקה הקלאסית. הרי במכניקה קלאסית אנו יודעים במדויק היכן החלקיק נמצא בכל רגע ומה מהירותו. אך למעשה זאת דעה שגוייה. מכניקת הקוונטים מספרת לנו איך באמת מתנהגים חלקיקים ברמה האטומית. היא פשוט לא מגדירה דברים שלא קיימים. כאשר מדברים על חלקיקים מיקרוסקופיים, מושגים כמו “מיקום מוגדר” ו”מסלול” מאבדים את משמעותם מפני שתנועה במסלול מסוים מהווה סתירה לאופי הגלי של החלקיקים. אפשר לראות זאת בבירור בניסוי עקיפה פשוט של אלקטרונים (איור 1).
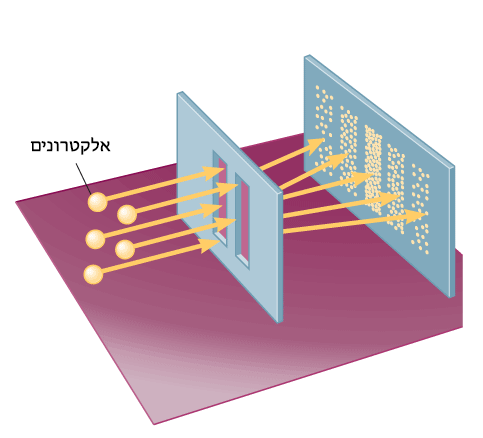
איור 1 – אלקטרונים עוברים דרך שני סדקים צרים ועל המסך נוצרת תבנית התאבכות
התבנית שנקבל כתוצאה מההתאבכות של שני הגלים שיצאו מהסדקים לא תהיה שווה לתבנית שתתקבל מחפיפה של תבניות התאבכות מכל סדק בנפרד. במילים אחרות, סכום ריבועי האמפליטודות של גלים המתקבלים מכל סדק בנפרד לא בהכרח שווה לסכום האמפליטודות שלהם בריבוע. בכתיב מתמטי:
\[|A+B|^2 \neq |A|^2 + |B|^2\]זה לא אומר שהגלים לא מתאבכים. זה רק אומר שצריך קודם לחבר אמפליטודות ורק אחר כך להעלות בריבוע, הרי בהחלט יכול להיות של-$A$ ול-$B$ יהיו סימנים שונים.
זה גם אומר שההסתברות לפגיעה של אלקטרון בנקודה כלשהי על המסך במקרה של שני סדקים לא שווה לסכום הסתברויות מכל סדק בנפרד (ההסתברות לפגיעה בנקודה מסוימת פרופורציונית לריבוע האמפליטודה של הגל הסופי). מכאן בהכרח נובעת המסקנה כי שני הסדקים משפיעים על תנועת החלקיק. זה לא עולה בקנה אחד עם מושג המסלול. הרי אם האלקטרון כל הזמן היה נע במסלול מסוים הוא היה עובר רק דרך סדק מסוים אחד – או דרך הסדק הראשון או דרך הסדק השני. תופעת העקיפה מוכיחה את ההפך – שני הסדקים משפיעים על התהליך.
מפתה לחשוב שאולי חלק אחד של האלקטרון עובר דרך הסדק הראשון בעוד שהחלק האחר שלו עובר דרך הסדק השני. אולם לא כך הדבר. אלקטרון, כמו כל חלקיק אחר, תמיד מתגלה כשלם עם מסה ומטען מסוימים האופייניים לו. כל זה מראה לנו שאלקטרונים, פרוטונים ושאר החלקיקים המיקרוסקופיים הם לא סתם חלקיקים – אי אפשר לדמות אותם לאיזשהם כדורים מזעריים. ככל שהמימדים קטנים יותר, כך התכונות הגליות הופכות לדומיננטיות יותר. לכן הצורה שבה תיארנו את האלקטרונים באיור הקודם איננה מדויקת ונועדה להמחשה בלבד.
עקרון אי-הוודאות של הייזנברג
מצד אחד, אמרנו שחסר טעם לדבר על מסלול תנועה במקרה של חלקיקים מיקרוסקופיים. מצד אחר, אנחנו מכירים את תא הערפל (איור 2) שבו ניתן לגלות חלקיקים על ידי העקבות שהם משאירים וזה לכאורה סותר את מה שאמרנו על מושג המסלול. כיצד, אם כן, ניתן ליישב את הסתירה?
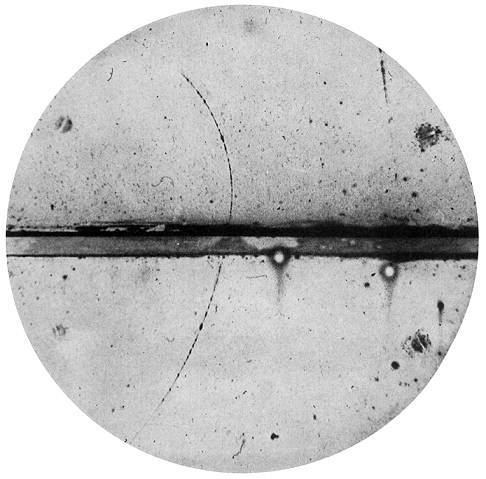
איור 2 – גילוי פוזיטרון בתא ערפל
ובכן, במקרים מסוימים אפשר לדבר על מסלול גם אם עוסקים בחלקיקים. ניזכר בשיעורי אופטיקה – אם מימדי המחסום הרבה יותר גדולים מאורך הגל אפשר בקירוב טוב להניח שהאור מתפשט בקווים ישרים (קרני אור). כך גם במקרה של אלקטרונים וחלקיקים מיקרוסקופיים אחרים – במצבים מסוימים מושגי המיקום והמסלול בקירוב טוב ישימים כשם שבמקרים מסוימים אפשר לתאר את התופעות הקשורות לאור על ידי אופטיקה גאומטרית.
מידת הדיוק איתה עוד אפשר לדבר על מיקום של חלקיק בנקודה מסוימת במרחב ניתנת על ידי עקרון אי-הודאות אותו ניסח ורנר הייזנברג. העיקרון קובע כי לחלקיק לא יכול להיות בו זמנית מיקום ותנע מוגדרים באותו הציר. מידת האי-ודאות עונה על התנאי הבא:
\[\Delta x \Delta p_x \gtrsim \hbar\]כאשר $\hbar = \frac{h}{2 \pi}$ ו-$h$ – קבוע פלאנק, השווה ל-$6.62 \cdot 10^{-34} \text{J} \cdot \text{s}$.
ככל שאחד מהגדלים, $x$ או $p_x$ מוגדר בצורה יותר מדויקת, כך יש יותר אי-ודאות לגבי הגודל האחר. יכול להיות גם מצב שבו אחד מהגדלים מוגדר היטב, מה שגורם לאחר להיות לא מוגדר כלל. נראה דוגמה פשוטה. נניח שחלקיק מסוים עובר דרך חריץ המאונך לכיוון תנועתו. לפני שהחלקיק עובר דרך החריץ, רכיב התנע שלו בציר $x$ מוגדר ושווה לאפס, כך שאין כלל אי-ודאות לגביו ($\Delta p_x = 0$), בעוד שקיימת אי-ודאות מוחלטת לגבי המיקום שלו (קואורדינטה $x$).
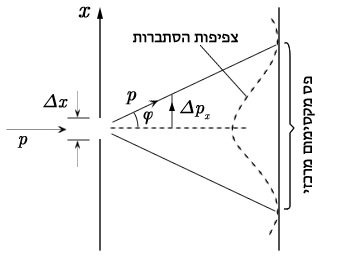
איור 3
ברגע שהחלקיק עובר דרך החריץ המצב משתנה. במקום אי-ודאות מוחלטת של $x$, מתקבלת אי-ודאות $\Delta x$ אך זה בא על חשבון הודאות ברכיב התנע $p_x$. אפשר להבין זאת כי בחריץ מתרחשת עקיפה, וכתוצאה מכך קיימת סבירות מסוימת שהחלקיק ינוע בטווח הזווית $2 \varphi$ כאשר $\varphi$ – זווית שבה מתקבל קו מינימום ראשון (אפשר להזניח את המקסימה מסדרים יותר גבוהים, כי עוצמתם נמוכה מזו של הפס המרכזי). במילים אחרות, מתקבלת אי-ודאות:
\[\Delta p_x = p \sin \varphi\]אבל אנו יודעים שהזוית בה מתקבל קו מינימום ראשון בעקיפה מקיימת:
\[\sin \varphi = \frac{\lambda}{\Delta x}\]לפיכך
\[\Delta p_x = p \frac{\lambda}{\Delta x}\]על פי היפותזת דה-ברויי, אורך הגל נמצא ביחס הפוך לתנע:
\[\lambda = \frac{h}{p}=\frac{2 \pi \hbar}{p}\]מכאן מקבלים:
\[\Delta x \Delta p_x = p \lambda = 2 \pi \hbar\]מה שתואם את עקרון אי-הודאות.
בחזרה לתא הערפל – נניח שרוחב השביל שיוצר החלקיק בתא ערפל הוא מסדר גודל של $10^{-2} \text{cm}$. אי-הודאות במהירות החלקיק, גם אם הוא הכי איטי (למשל $1 \text{km/s}$), תיהיה רק $7 \text{m/s}$, מה שזניח ביותר.
בנוסף לכך, ניתן להסביר מדוע אלקטרון לא נופל על הגרעין – אילו האלקטרון היה נופל על הגרעין, התנע והמיקום שלו היו הופכים להיות מוגדרים (שווים לאפס), מה שכמובן בלתי אפשרי לפי עקרון אי-ודאות.
חשוב להבין שלא מדובר בקשיים טכניים כלשהם. העיקרון משקף את הדואליות האובייקטיבית של חלקיקים ולא ניתן להסיר את אי-הודאות גם בניסוי הכי אידאלי עם מכשירים הכי אידאליים. תמיד כאשר רוצים למצוא גודל אחד בצורה יותר מדויקת, נאלצים לוותר על הודאות לגבי הגודל האחר. ראינו זאת בדוגמה הקודמת – אם מקטינים את רוחב החריץ על מנת לקבוע בדיוק את מיקום החלקיק, אנו מאבדים מידע אודות רכיב התנע שלו. ככל שהחריץ צר יותר, כך הגל העוקף אותו יוצא יותר רחב ולכן אי-הודאות לגבי רכיב התנע גדלה.
קוונטיזציה
מלבד חישוב הסתברות למציאת חלקיק בנקודות שונות במרחב למשוואת שרדינגר יש ערך נוסף – ניתן באמצעותה לקבל את חוקי הקוונטיזציה של אנרגיה.
בגלל המשמעות הפיזיקלית של פונקציית הגל, היא חייבת להיות חד ערכית ורציפה בכל תחום הגדרתה. במשוואת שרדינגר מופיעה האנרגיה הכוללת $E$ של החלקיק. מתורת המשוואות הדיפרנציאליות אפשר להוכיח שלמשוואה יהיה פתרון שיענה על תנאי הרציפות והחד-ערכיות רק עבור ערכים מסוימים של $E$. מציאת ערכים אלו מהווה בעיה מתמטית יחסית קשה, לכן נמנע מפירוט מתמטי מתי שזה אפשרי. מה שכן חשוב להדגיש זה את העובדה שפונקציית גל חייבת להיות “מנורמלת”, כלומר:
האינטגרציה מתבצעת על כל תחום ההגדרה של הפונקציה. באמצעות האינטגרל אנו מסכמים את כל ההסתברויות בכל הנפחים המזעריים האפשריים, כלומר אנו מחשבים את ההסתברות למצוא את החלקיק באיזושהי נקודה במרחב. מפני שהחלקיק חייב להיות איפשהו, זאת הסתברות של מאורע ודאי, כלומר היא חייבת להיות שווה ל-1.
תנועה של חלקיק חופשי
נראה כמה דוגמאות לתנועה של חלקיקים מיקרוסקופיים כאשר התכונות הגליות הן אלה שקובעות את תנועתם ואת האנרגיה שלהם. מאוד חשוב להבדיל בין שני מקרים: מקרה שבו על החלקיק פועלים כוחות ומקרה בו לא פועלים כוחות כלל (תנועה חופשית). ההבדל טמון בעובדה שהאנרגיה $E$ של החלקיק לא יכולה לקבל כל ערך אם פועלים על החלקיק כוחות. מסתבר שאם מלבד האנרגיה הקינטית לחלקיק יש גם אנרגיה פוטנציאלית $U$ (או יותר נכון, החלקיק הוא חלק ממערכת בה אגורה אנרגיה פוטנציאלית), האנרגיה הכוללת שלו $E$ תהיה מקוונטטת. כזכור, גודל פיזיקלי נקרא מקוונטט אם הוא יכול לקבל רק ערכים בדידים.
לשם פשטות, נדון במקרה בו חלקיק בעל מסה $m$ נע במהירות קבועה שקטנה משמעותית ממהירות האור $v \ll c$ לאורך ציר כלשהו שנקרא לו $x$. לא פועלים על החלקיק שום כוחות – התנועה היא חופשית. התנע של החלקיק הוא $p=mv$ ואורך הגל שלו (גל דה-ברויי) הינו $\lambda = \frac{h}{p}$. הגל מתפשט לאורך ציר $x$ ומספר הגל הינו $k=\frac{2 \pi}{\lambda}$. כידוע מלימודי גלים, ניתן לבטא את משוואת הגל בעזרת התדירות הזוויתית $\omega$ ומספר הגל $k$ בצורה הבאה:
\[s=A \cos (k x - \omega t)\]כאשר $A$ – אמפליטודה של הגל.
במכניקת הקוונטים הביטוי לפונקציית הגל קצת שונה:
\[\Psi = A (\cos \alpha + i \sin \alpha)\]כאשר
\[\alpha = kx - \omega t = \frac{p x}{\hbar} - \frac{E t}{\hbar}\]כאן $E$ זאת האנרגיה של החלקיק, $p$ – התנע שלו ו-$i$ – היחידה המדומה ($i^2=-1$).
כבר אמרנו שההסתברות למציאת חלקיק באזור כלשהו במרחב פרופורציונית לריבוע הערך המוחלט של פונקציית הגל. אם למדתם על מספרים מרוכבים, אתם בוודאי יודעים שריבוע הערך המוחלט של מספר מרוכב שווה למספר המרוכב כפול הצמוד שלו (המספר המרוכב עם סימן נגדי בחלק המדומה) – $|z|^2=z\bar{z}$. כך גם לגבי צפיפות ההסתברות:
\[\begin{align*} |\Psi|^{2} & =\Psi\Psi^{*}=A\left(\cos\alpha+i\sin\alpha\right)\cdot A\left(\cos\alpha-i\sin\alpha\right)\\ & =A^{2}\left(\cos^{2}\alpha-i\cos\alpha\sin\alpha+i\sin\alpha\cos\alpha+\sin^{2}\alpha\right)\\ & =A^{2} \end{align*}\]אם כן, אנו מקבלים צפיפות הסתברות שאיננה תלויה בזמן – קבועה. המשמעות הפיזיקלית של תוצאה זו היא שיש הסתברות שווה למצוא את החלקיק בכל נקודה על ציר $x$. זה תואם את עקרון אי-הודאות של הייזנברג, כי לפיו אם לחלקיק תנע נתון הידוע בוודאות, תהיה אי-ודאות מוחלטת לגבי המיקום שלו.
כל מה שנשאר זה למצוא ביטוי לאנרגיה של החלקיק. אורך גל דה-ברויי, כאמור, הינו $\lambda = \frac{h}{m v}$, לכן $v=\frac{h}{m \lambda}$. האנרגיה הכוללת של החלקיק היא האנרגיה הקינטית שלו ולפי הקשר הקודם מתקיים:
\[E=\frac{mv^2}{2}=\frac{h^2}{2 m \lambda^2}\]בור פוטנציאל אינסופי
כעת נראה כיצד החלקיק ינוע אם נגביל את התנועה שלו. נניח שהחלקיק נע לאורך ציר $x$. מנקודה $x=0$ ועד לנקודה $x=L$ החלקיק יכול לנוע בצורה חופשית. אולם הוא איננו יכול לצאת מהאזור $(0,L)$. זה אומר שבגבולות הטווח הזה, כלומר בנקודות $x=0$ ו-$x=L$ האנרגיה הפוטנציאלית היא אינסופית. תוכלו לדמיין שהחלקיק נמצא בתחתית מיכל כלשהו עם דפנות מחזירים אידאליים שגובהם אינסופי. במקרה כזה אומרים שהחלקיק נמצא בבור פוטנציאל אינסופי. כמובן שאין באמת כאלה בורות כפי שאין משטחים חסרי חיכוך, גופים שחורים לגמרי וכו’. אך למשל כאשר חוקרים מוליכות של מתכות מסוימות, אפשר לתאר אלקטרונים כחלקיקים שנמצאים בבור פוטנציאל כאשר גובה החסם הפוטנציאלי שווה לעבודת היציאה של המתכת. לפיכך, המצב הזה מהווה מודל מופשט של בעיה אמיתית וחשובה מאוד.
משום ש-$\Psi$ תלוייה רק בקואורדינטה אחת $x$, משוואת שרדינגר תיראה כך:
\[\frac{d^2 \Psi}{dx^2}+\frac{2 m}{\hbar^2}(E-U) \Psi=0\]בבעיה הנדונה תנועתו של החלקיק הינה מוגבלת. הוא נמצא במלכודת מלבנית ואיננו יכול לברוח ממנה. נסכם את התנאים שהבעיה מציבה. האנרגיה הפונציאלית תלויה בקואורדינטה $x$: אם $x < 0$ או $x > L$ האנרגיה הפוטנציאלית שווה $U = \infty$; אם $0 \leq x \leq L$ אזי $U=0$ (איור 4). מה זה אומר מבחינת פונקציית הגל? זה אומר שמחוץ לגבולות היא שווה לאפס, כי ריבוע פונקציית הגל צריך להיות אפס (הסתברות אפסית למציאת החלקיק מחוץ לבור). נוכל לרשום:
\[\left\{\begin{matrix} \Psi(0)=0, \\ \Psi(L)=0 \end{matrix}\right. \tag{1}\]
איור 4 – בור פוטנציאל אינסופי
התנאים שהצבנו לעיל קובעים את פתרונות המשוואה. במקרה שבו $\Psi$ לא שווה בדיוק לאפס, כלומר איפה שיש סיכוי למצוא את החלקיק (שם, כאמור, $U=0$), המשוואה תיראה כך:
\[\frac{d^2 \Psi}{d x^2} + \frac{2 m}{\hbar^2} E \Psi = 0 \tag{2}\]אם נסמן $\omega^2 = \frac{2 m E}{\hbar^2}$ המשוואה תיראה יותר מוכרת למי שזוכר את הנושא של מתנד הרמוני:
\[{\Psi} ' ' + \omega^2 \Psi = 0\]פתרון משוואה כזאת הוא:
\[\Psi(x)=a \sin (\omega x + \varphi)\]כאשר הקבועים $\varphi$ ו-$\omega$ נבחרים כך שהתנאים שסומנו ב-(1) יתקיימו.
ראשית, מהתנאי $\Psi(0) = 0$ מקבלים:
\[\Psi(0)=a \sin \varphi = 0\]מכאן ש-$\varphi$ חייב להיות שווה לאפס (כי $a \neq 0$).
כמו כן, התנאי השני צריך להתקיים:
\[\Psi(L)=a \sin (\omega L) = 0\]מה שאפשרי רק אם
\[\omega L = \pm n \pi ~~~~ (n=1,2,3,…) \tag{3}\]($n=0$ לא מתאים מפני שאז $\Psi = 0$, כלומר החלקיק לא נמצא בשום מקום, וזה כמובן לא נכון).
מ-(3) אנחנו יכולים להסיק שפתרונות המשוואה (2) יהיו בעלי משמעות פיזיקלית רק עבור ערכים מסוימים של האנרגיה $E$. הערכים הללו מקיימים:
\[\omega^2=\frac{2 m}{\hbar^2} E_n=\frac{\pi^2}{L^2} n^2 \quad (n=1,2,3,…)\]אם כן, קיבלנו קוונטיזציה של אנרגיה ללא שום הנחות יסוד מיותרות (בדומה לאלו שבוהר נאלץ להניח):
\[E_n = \frac{\pi^2 \hbar^2}{2 m L^2} n^2 = \frac{n^2 h^2}{8 m L^2} \quad (n=1,2,3,…)\]לערכים המקוונטטים של אנרגיה $E_n$ קוראים רמות אנרגיה. למספר $n$ שבאמצעותו מקבלים את רמות האנרגיה קוראים מספר קוונטי.
ניתן להציג את רמות האנרגיה באמצעות הדיאגרמה הבאה:

איור 5 – רמות אנרגיה של חלקיק הכלוא בבור פוטנציאל אינסופי
(שוב נזכיר כי לחלקיק לא יכולה להיות אנרגיה השווה לאפס, מפני שזאת תיהיה הפרה של עקרון אי-הודאות וגם כי פונקציית הגל מתאפסת עבור $n=0$).
מכל האמור לעיל נובע שחלקיק הכלוא בבור פוטנציאל יכול להימצא אך ורק ברמות אנרגיה בדידות. נהוג לומר שהחלקיק נמצא במצב קוונטי עמיד $n$. זה נועד להדגיש את העובדה שמצב החלקיק בעל האנרגיה $E_n$ הינו מצב סטציונרי, כלומר הוא לא משתנה בזמן ובהעדר כל השפעה חיצונית החלקיק מסוגל להימצא במצב כזה במשך זמן לא מוגבל. נדגיש שוב כי החלקיק יכול לקבל רק ערכים בדידים של אנרגיה. כמו כן, על מנת למנוע בלבול מיותר, נדגיש שכאשר אומרים מצב עמיד אין הכוונה לכך שהחלקיק הוא “עמיד” ולא נע. מה שעמיד כאן זה צפיפות ההסתברות למציאת החלקיק וגם רמות האנרגיה – הם לא משתנים בזמן.
נעריך את ההפרשים בין רמות האנרגיה עבור חלקיקים שונים. הפרש בין שתי רמות אנרגיה סמוכות שווה
\[\Delta E = E_{n+1} - E_n =\frac{h^2}{8 m L^2}[(n+1)^2-n^2]=(2n+1)\frac{h^2}{8 m L^2}\]נניח שיש לנו חלקיק שמסתו מסדר גודל מסה של מולקולה ($\sim 10^{-26} \text{kg}$) ורוחב הבור $L$ הוא בסביבות $10 \text{cm}$ (מולקולות גז בתוך מיכל). אזי ההפרש בין רמות אנרגיה יהיה:
\[\begin{align*} \Delta E & =(2n+1)\frac{h^{2}}{8mL^{2}}=\frac{(6.62\cdot10^{-34})^{2}}{8\cdot10^{-26}\cdot10^{-4}}\\ & =(2n+1)\cdot5.5\cdot10^{-40}\text{J}=(2n+1)\cdot3.4\cdot10^{-21}\text{eV} \end{align*}\]לרמות אנרגיה כה צפופות אפשר להתייחס בקירוב טוב כאל ספקטרום רציף של אנרגיות. אמנם קוונטיזציה של אנרגיה קיימת, אך התוצאה כמעט ולא שונה ממה שהיינו מצפים לפי מכניקה קלאסית – אנרגיה רציפה. רואים גם שכאשר $L \to \infty$ סדרת רמות האנרגיה הופכת לממש רציפה מפני שאז $\Delta E \to 0$.
תוצאה דומה תתקבל אם באותו הבור יהיה אלקטרון (מסתו $9.1 \cdot 10^{-31} \text{kg}$). זה יכול להיות למשל אלקטרון במתכת:
\[\begin{align*} \Delta E & =\frac{(6.62\cdot10^{-34})^{2}}{8\cdot9.1\cdot10^{-31}\cdot10^{-4}}=(2n+1)\cdot6\cdot10^{-36}\text{J}\\ & =(2n+1)\cdot3.8\cdot10^{-17}\text{eV} \end{align*}\]גם כאן הכול צפוף. אבל אם הבור יהיה מסדר גודל של מימדי האטום ($\sim 10^{-10} \text{m}$), המצב יהיה שונה:
\[\Delta E = \frac{(6.62 \cdot 10^{-34})^2}{8 \cdot 9.1 \cdot 10^{-31} \cdot 10^{-20}}=(2n + 1) \cdot 6 \cdot 10^{-18} \text{J} \approx (2n + 1) \cdot 36 \text{eV}\]במקרה כזה הדיסקרטיות של רמות האנרגיה יותר מובהקת.
נראה כעת מה קורה עם פונקציית הגל. מ-(3) מקבלים:
\[\Psi_n (x) = a \sin \frac{n \pi x}{L}\]על מנת למצוא את המקדם $a$, ניזכר בעובדה שפונקציית גל חייבת להיות מנורמלת, כלומר:
\[\int_{0}^{L} |\Psi_n (x)|^2 dx=1\\ a^2 \int_{0}^{L} \sin^2 \frac{n \pi x}{L} dx = 1\](אם לא למדתם חשבון דיפרנציאלי ואינטגרלי, אתם יכולים לדלג על ההסבר של פתרון האינטגרל הזה ולראות ישר את התוצאה).
בקצוות טווח האינטגרציה (למעשה בקצוות בור הפוטנציאל) הפונקציה שמתחת לאינטגרל מתקרבת לאפס. לפיכך אפשר למצוא את האינטגרל על ידי הכפלה של הערך הממוצע של $\sin^2 (n \pi x / L)$ (השווה ל-$\frac{1}{2}$) באורך הקטע $L$ (ראה את משפט הערך הממוצע של לגראנז’ בגירסתו האינטגרלית). לכן $a^2 \cdot L \cdot \frac{1}{2}=1 \to a = \sqrt{2/L}$. אם כן, פונקציית הגל תיראה כך:
\[\Psi_n (x) = \sqrt{\frac{2}{L}} \sin \frac{n \pi x}{L} ~~~~ (n=1,2,3,…)\]גרפים של פונקציית גל $\Psi_n(x)$ מוצגים באיור 6 (א). באיור 6 (ב) מוצגת צפיפות הסתברות למציאת חלקיק בנקודות שונות בבור.
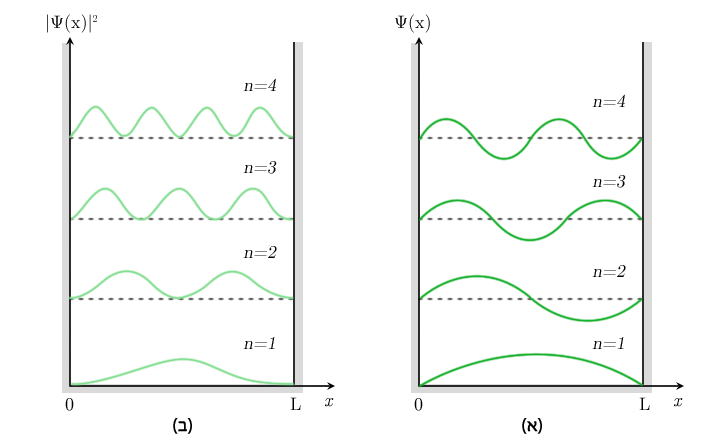
גרפים של $ si(x)$ ושל $| si(x)|^2$ עבור מספרים קוונטיים שונים
מהגרפים אפשר להבין שלמשל חלקיק במצב קוונטי $n=2$ לא יכול להימצא באמצע הבור, בעוד שההסתברויות למציאתו בחלק הימני או השמאלי של הבור שוות. ברור שהתנהגות כזאת לא עולה בקנה אחד עם רעיונות המסלול והמיקום הקלאסיים שאנו רגילים אליהם. אך כאמור, התנהגות החלקיקים בעולם המיקרוסקופי שונה מהתנהגות הגופים בעולם המאקרוסקופי שאותו אנו חווים. אנו רואים גם כי אחת התכונות החשובות ביותר של כל חלקיק – האנרגיה שלו – היא מקוונטטת, והמסקנה הזאת לא תלוייה בצורת בור הפוטנציאל.
נראה כיצד קוונטיזציה של אנרגיה תלוייה במספר הקוונטי $n$. לשם כך נמצא את היחס $\Delta E / E_n$:
עבור ערכים גדולים מאוד של $n$ מקבלים $2 n + 1 \approx 2 n$, כלומר:
\[\frac{\Delta E}{E_n}=\frac{2}{n}\]אפשר לראות כי במקרה של $n \gg 1$ היחס מקיים $\Delta E / E_n \ll 1$. נוכל לרשום זאת גם בצורה הבאה:
\[\Delta E \ll E_n\]זאת אומרת שעבור מספרים קוונטיים גדולים מאוד הרמות מצטופפות. במילים אחרות, ערכים גדולים של $n$ נותנים תוצאות יותר קרובות לאלו שמנבא המכניקה הקלאסית ורמות האנרגיה הופכות להיות קוואזי-רציפות. זהו עקרון ההתאמה שנוסח על ידי נילס בוהר בשנת 1923:
עבור מספרים קוונטיים גדולים המערכת הקוונטית שואפת אל הגבול הקלאסי – תוצאותיה מתלכדות עם תוצאות ממכניקה קלאסית.
בניסוח יותר כללי העקרון קובע כי קיים קשר בין כל תורה פיזיקלית שמהווה הכללה של תורה קלאסית לבין התורה הקלאסית עצמה – במצבים גבוליים מסוימים התאוריה החדשה צריכה לעבור לישנה. לדוגמה, משוואות קינמטיות ודינמיות מתורת היחסות הפרטית מתלכדות עם נוסחאות ממכניקה ניוטונית כאשר מדובר במהירויות שהרבה יותר נמוכות ממהירות האור ($v \ll c$). דוגמה נוספת היא אופטיקה – תוצאות האופטיקה הגלית מתלכדות עם תוצאות האופטיקה הגאומטרית כאשר ניתן להזניח את אורך הגל ביחס לכל אורך אחר שמופיע בבעיה ולהניח כי $\lambda \to 0$. בין מכניקת הקוונטים לבין המכניקה הקלאסית הגבול מתקבל בהזנחה של הגודל $h$ (כלומר כאשר ניתן להניח ש-$h \approx 0$).
אטום המימן
באטום המימן או באטום דמוי-מימן האנרגיה הפוטנציאלית של האלקטרון שווה
\[U=- k \frac{Z e^2}{r}\]כאשר $Z e$ – מטען הגרעין ו-$r$ – מרחק האלקטרון מהגרעין. במקרה זה, משוואת שרדינגר תיראה כך:
\[\Delta \Psi + \frac{2 m_e}{\hbar^2} \left (E+ k \frac{Z e^2}{r} \right ) \Psi = 0\]כאן $\Delta$ הינו אופרטור לפלס – דרך יותר פשוטה לכתוב נגזרת שנייה לפי שלושה משתנים.
ניתן להוכיח שהמשוואה הקודמת נותנת פתרונות מתאימים (כדרוש – חד ערכיים, סופיים ורציפים) במקרים הבאים:
- עבור כל ערך חיובי של $E$
- עבור ערכים בדידים שליליים של אנרגיה הנתונים על ידי הביטוי:
המקרה הראשון ($E > 0$) מתאים למצב שבו אלקטרון עובר בקרבת הגרעין ולאחר מכן מתרחק ממנו לאינסוף. המקרה השני ($E < 0$) מתאים למצב שבו האלקטרון שוהה בתוך האטום. אתם יכולים לראות שהביטוי לאנרגיה המקוונטטת זהה לביטוי שמתקבל מהמודל של בוהר. ההבדל הוא שבמכניקת הקוונטים קיבלנו את הביטוי רק מעצם זה שהנחנו כי משוואת שרדינגר מתארת נכון את תנועת החלקיקים בעולם המיקרוסקופי. לעומת זאת בוהר נאלץ להניח הנחות יסוד שונות בכדי להגיע לאותה התוצאה.
אך קוונטיזציה של אנרגיה זה לא הדבר היחידי שמתקבל מהמשוואה שהוצגה לעיל. מסתבר כי בכל אטום, ולא רק באטום המימן, התנע הזוויתי של האלקטרון $L_l$ יכול לקבל רק ערכים בדידים:
\[L_l = \sqrt{l (l+1)} \hbar\]כאשר $l$ – מספר התנע הזוויתי, שעבור מספר קוונטי $n$ נתון יכול לקבל ערכים:
\[l=0,1,2,…, n-1\]כזכור, במודל של בוהר התנע הזוויתי המקוונטט ניתן על ידי הביטוי $L_n= m v r = n \hbar ~~~~ (n=1,2,3,…)$. כפי שניתן לראות, הביטוי הזה שונה מהביטוי שקיבלנו קודם – הביטוי של בוהר כולל תלות במספר קוונטי $n$ בלבד, בעוד שהביטוי הקודם כולל תלות ב-$l$. חשוב להבין שמספר התנע הזוויתי יכול לקבל ערכים שלמים עד $n-1$. לפי מכניקת הקוונטים, בכל אטום אפשרי מצב שבו לאלקטרון יהיה תנע זוויתי $L_l$ השווה לאפס. במודל של בוהר זה לא אפשרי, כי לפיו האלקטרון לא יכול לעבור דרך הגרעין. במילים אחרות, לפי המודל של בוהר מצבים של $l=0$ בלתי אפשריים. ניסויים רבים הוכיחו שבהחלט קיימים מצבים בהם לאלקטרון אין תנע זוויתי. לפיכך המודל של בוהר נכשל כאן.
ישנן כמה מוסכמות בפיזיקה האטומית שנועדו לתאר את מצבי האלקטרון באטום:
- אם $l=0$, מצב האלקטרון נקרא מצב $s$
- אם $l=1$, מצב האלקטרון נקרא מצב $p$
- כאשר $l = 2, 3, …$ המצבים מקבלים אותיות $d$, $f$ וכו’ בסדר האלפבית הלטיני
מהי המשמעות הפיזיקלית של מסלולי בוהר?
ננתח דוגמה של אלקטרון במצב $s$ באטום המימן כאשר $n=1$, כלומר כאשר האטום נמצא ברמת היסוד. באמצעות משוואת שרדינגר ניתן להוכיח שההסתברות למציאת האלקטרון בנקודה מסוימת בתוך האטום תלוייה במקרה זה אך ורק במרחקו $r$ מהגרעין. זה אומר שבכל הנקודות הנמצאות על ספירה בעלת רדיוס $r$ שמרכזה בגרעין יש סיכוי שווה למצוא את האלקטרון. במילים אחרות, לצפיפות ההסתברות יש סימטריה ספרית. מסתבר שניתן לתאר את ההסתברות $P(r)$ למציאת חלקיק במרחק נתון מהגרעין על ידי העקומה הבאה:
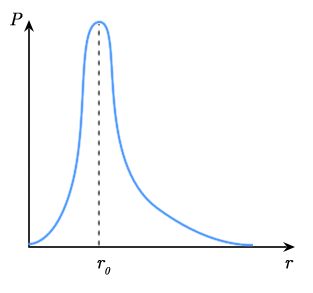
איור 7
לפונקציית ההסתברות $P(x)$ יש מקסימום ב-$r_0$ ומסתבר שזה מתאים לרדיוס בוהר ראשון. לפיכך, אפשר לומר את הדבר הבא:
מסלולי בוהר של אלקטרון באטום הינם מקומות גאומטריים של נקודות בהם ההסתברות למציאת האלקטרון היא הכי גבוהה
שימו לב שמכניקת הקוונטים לא אוסרת על האלקטרון להימצא בכל רדיוס אחר. פשוט הסיכוי למצוא אותו ברדיוסים “לא מותרים” נמוך יותר. במובן זה המודל של בוהר שוב נכשל, כי לפיו ישנם רק רדיוסים מותרים ולא שום דבר “באמצע”.