כידוע, על כל חלקיק הנע בשדה מגנטי פועל כוח לורנץ. זה קורה במנועים חשמליים, במאיצי חלקיקים טעונים, בשדה מגנטי של כדה”א וכו’. ניזכר כי גודל כוח לורנץ הוא:

\[|\mathbf{F_l}| = q |\mathbf{v}| |\mathbf{B}| \sin \alpha\]

כאשר $q$ – מטען החלקיק, $\mathbf{v}$ – מהירותו, $\mathbf{B}$ – השדה המגנטי ו-$\alpha$  – הזווית שבין הווקטורים $\mathbf{B}$ ו-$\mathbf{v}$.

וקטור כוח לורנץ תמיד מאונך לווקטורי המהירות והשדה המגנטי. קל למצוא את הכיוון של הווקטור באמצעות כלל יד ימין: מכוונים את אצבעות יד ימין בכיוון בו הייתם מסובבים את הווקטור $\mathbf{v}$ אל הווקטור $\mathbf{B}$ (בזווית הקטנה) ואז האגודל יצביע בכיוון הכוח (איור 1). במקרה של מטען שלילי (כמו למשל האלקטרון) עושים את אותו הדבר רק עם יד שמאל.

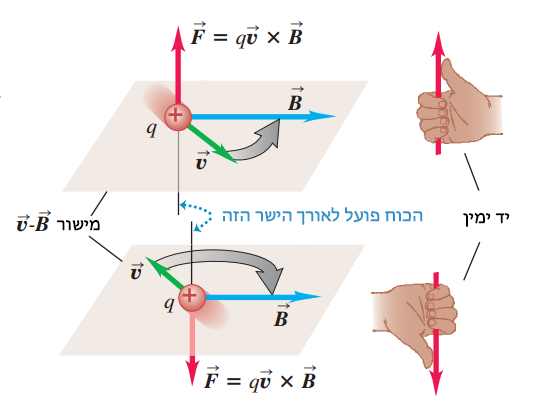
איור 1 – קביעת כיוונו של כוח לורנץ עפ"י כלל יד ימין

נראה עתה כמה דוגמאות לשימוש בכוח לורנץ.

1. חלקיק שמטענו $+q$ נכנס לשדה מגנטי אחיד שעוצמתו $\mathbf{B}$. וקטור המהירות של החלקיק בעת הכניסה לשדה היה מאונך לווקטור $\mathbf{B}$ (איור 2). תאר כיצד ינוע החלקיק.

מכיוון שכוח לורנץ כל הזמן פועל במאונך לווקטור המהירות, הוא לא מסוגל לשנות את גודל המהירות אלא רק את הכיוון שלה. זאת אומרת שהחלקיק מקבל תאוצה צנטריפטלית $\mathbf{a}_c$ אשר גורמת לו לנוע בתנועה מעגלית קצובה. ניתן למצוא את הרדיוס התנועה המעגלית באמצעות החוק השני של ניוטון:

\[|\mathbf{F}_l| = m |\mathbf{a}_c|\]

או

\[q |\mathbf{v}| |\mathbf{B}| = m \frac{|\mathbf{v}|^2}{R}\]

מכאן שהרדיוס:

\[R = \frac{m |\mathbf{v}|}{q |\mathbf{B}|}\]

($m$ – מסת החלקיק הטעון)

נשים לב כי כוח לורנץ לא מבצע עבודה מפני שהוא מאונך לווקטור המהירות בכל רגע ורגע (לכן גם אין שינוי באנרגיה הקינטית של החלקיק).

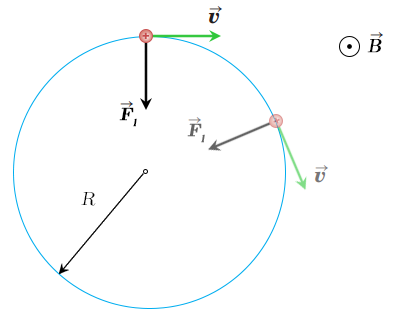
איור 2 – חלקיק טעון חיובית נע בתוך שדה מגנטי בתנועה מעגלית קצובה

2. נראה עתה מה קורה עם מוליך מתכתי הנושא זרם כאשר הוא נמצא בשדה מגנטי. כפי שאתם יודעים, במוליכים מתכתיים הזרם מורכב מאלקטרונים הנעים אל עבר הפוטנציאל החיובי (בכיוון מנוגד לכיוון המוסכם של הזרם). נניח כי הזרם זורם מימין לשמאל (האלקטרונים נעים משמאל לימין). כתוצאה מהשדה המגנטי על האלקטרונים יפעל כוח לורנץ כלפי מטה (איור 3).

איור 3

מכיוון שהאלקטרונים הללו חופשיים הם יתחילו לנוע בהשפעת כוח לורנץ. זה יגרום להצטברותו של מטען שלילי בתחתית המוליך ומכאן שיהיה מחסור במטען שלילי בחלק העליון. פירוש הדבר שייווצרו שדה חשמלי $\mathbf{E}$ (שיהיה מכוון כלפי מטה) ומתח (הפרש פוטנציאלים) $U$. אפקט זה ידוע בשם אפקט הול. תנועת האלקטרונים בניצב לכיוון הזרם תמשיך עד שהכוח החשמלי שיפעל האלקטרונים (כתוצאה מהשדה החשמלי) לא ישתווה בגודלו לכוח לורנץ (איור 4):

\[\mathbf{F}_e=-\mathbf{F}_l\]

או

\[e |\mathbf{E}|=e|\mathbf{v}||\mathbf{B}|\]

(כאשר $e$ – מטען האלקטרון, $\mathbf{v}$ – המהירות הממוצעת של אלקטרון, $\mathbf{B}$ – השדה  המגנטי).

מכאן פשוט למצוא את עוצמת השדה החשמלי שנוצר בגלל הפרדת המטענים:

\[|\mathbf{E}|=|\mathbf{v}||\mathbf{B}|\]

ואת המתח:

\[U=|\mathbf{E}| d =|\mathbf{v}||\mathbf{B}| d\]

(כאשר $d$ – רוחב המוליך).

איור 4

מצד אחר, קיים קשר בין המהירות הממוצעת $\mathbf{v}$ לבין עוצמת הזרם $I$:

\[I= e n |\mathbf{v}| S\]

לכן

\[|\mathbf{v}| = \frac{I}{e n S}\]

כאשר $n$ – מספר האלקטרונים החופשיים ביחידת נפח אחת של המוליך ו-$S$ – שטח החתך של המוליך. מפה אפשר לקבל את הביטוי הסופי להפרש הפוטנציאלים:

\[U= |\mathbf{v}| |\mathbf{B}| d = \frac{d}{e n S} I |\mathbf{B}|\]

עוד בשנת 1820 אנדרה אמפר הראה כי גודל הכוח $\mathbf{F}$ הפועל על קטע תיל קצר באורך וכוון $\Delta \mathbf{l}$ הנושא זרם $I$ הוא:

\[|\mathbf{F}| = |I \Delta \mathbf{l}| |\mathbf{B}| \sin \alpha\]

(כאשר $\alpha$ הזווית שיוצר וקטור הקטע עם וקטור השדה המגנטי).

הכוח הזה (הידוע גם ככוח אמפר) מאונך לווקטור הקטע ולווקטור השדה המגנטי, ואת כיוונו ניתן לקבוע עפ”י כלל יד ימין (איור 5). מסתבר גם שכוח אמפר אינו אלא השקול של כוחות לורנץ הפועלים על האלקטרונים. יש לציין כי העובדה שקיים שדה חשמלי $\mathbf{E}$ המפסיק את ההטייה של האלקטרונים לא אומרת שמתבטל הכוח השקול, וזאת מפני שהכוחות החשמליים פועלים הן על היונים החיוביים של המתכת והן על האלקטרונים ולכן בסך הכול הם מקזזים זה את זה כאשר מסתכלים על התיל כולו. כוחות הלורנץ שבסך הכול נותנים את הכוח הפועל על קטע התיל עדיין נשארים. אם כן, כוח לורנץ הפועל על האלקטרונים הנעים בתיל מועבר לתיל עצמו, ואם אין שום דבר המחזיק אותו, התיל יאיץ.

איור 5 – כוח אמפר שווה לשקול כוחות הלורנץ הפועלים על כל האלקטרונים במוליך

1. לבסוף, נדון במקרה בו מוליך מתכתי לא טעון ולא נושא זרם נע בשדה מגנטי אחיד.

מניסויים מסתבר כי במקרה זה, בין קצות המוליך נוצר הפרש פוטנציאלים, ואם נחבר אליו תיל מוליך, יתחיל לזרום דרכם זרם חשמלי שנקרא גם זרם מושרה. (על עקרון זה מבוססים רוב הגנרטורים ההופכים אנרגיה מכנית לחשמלית).
מדוע וכיצד נוצר הזרם המושרה? נניח כי קטע תיל שאורכו $l$ נע במהירות $\mathbf{v}$ במאונך לשדה מגנטי $\mathbf{B}$ (איור 6). האלקטרונים החופשיים נעים יחד עם התיל, לכן יפעל עליהם כוח לורנץ. במקרה שלנו, זה יגרום לאלקטרונים לנוע מלמטה למעלה (איור 6 א’). כמו באפקט הול, גם כאן התנועה הזאת תיפסק כאשר הצטברות המטען השלילי תיצור שדה מספיק חזק שיאזן את כוח לורנץ (איור 6 ב’).

איור 6

אם נחבר את קצות התיל אל מוליך נייח כך שהתיל יוכל לנוע עליו באופן חופשי (איור 7), האלקטרונים שיצטברו למעלה יוכלו לעבור למטה רק דרך המוליך הנייח, כי בתיל כוח לורנץ ימנע מהם לעבור ישירות למטה. הפרש הפוטנציאלים הנוצר לא יקטן מפני שהאלקטרונים בתיל שוב ושוב יתחילו לעלות כלפי מעלה בגלל כוח לורנץ.

איור 7

אם כן, אנו רואים שבמוליכים הללו זורם זרם חשמלי. את תפקיד המקור משחק התיל הנע, שבתוכו על האלקטרונים פועל כוח לורנץ (שמשחק את תפקיד הכא”מ). הפרש הפוטנציאלים הנוצר בין קצות התיל מאפשר זרימת זרם קבוע במוליך החיצוני.

מה ניתן לומר על העבודה שמבצע כוח לורנץ? מצד אחד, וקטור כוח לורנץ תמיד מאונך לווקטור המהירות, לכן הוא לא יכול לבצע עבודה. מצד אחר, כפי שראינו, הודות לכוח לורנץ נוצר הפרש פוטנציאלים בתיל הנע בתוך שדה מגנטי, כלומר כוח לורנץ כן מבצע עבודה.
ננסה ליישב את הסתירה בכך שננתח לעומק את מה שקורה בתוך התיל עצמו. נוסיף לשם כך מערכת צירים (איור 8): ציר $x$ יהיה בכיוון שבו נע התיל וציר $y$ יהיה בכיוון התיל כלפי מעלה. נסמן ב-$\mathbf{v}_x$ את מהירות האלקטרון בגלל תנועת התיל. ברגע שהתיל מתחיל לנוע, גם האלקטרון שנמצא בתוכו מתחיל לנוע ומתחיל לפעול עליו כוח לורנץ. כתוצאה מכך האלקטרון נע גם כלפי מעלה, בכיוון ציר $y$ במהירות $\mathbf{v}_y$. ברור כי המהירות השקולה של האלקטרון שווה

\[\mathbf{v}=\mathbf{v}_x+\mathbf{v}_y\]

איור 8

וקטור כוח לורנץ מאונך לווקטור המהירות השקולה $v$ ולכן הוא איננו מכוון לאורך ציר $y$ אלא יוצר זווית מסוימת עמו.
נפרק את כוח לורנץ $\mathbf{F}_l$ לרכיבים $\mathbf{F}_x$ ו-$\mathbf{F}_y$. ברור כי הכוח $\mathbf{F}_l$ לא מבצע עבודה מפני שהוא מאונך למהירות האלקטרון. אולם עבודת הכוחות $\mathbf{F}_x$ ו-$\mathbf{F}_y$ שונה מאפס. הכוח $\mathbf{F}_y$ מבצע עבודה חיובית, בעוד שהכוח $\mathbf{F}_x$ – עבודה השווה בגודלה לזו שמבצע $\mathbf{F}_y$ אך עם סימן מינוס.

למרות שבסך הכול עבודת הרכיבים שווה לאפס, לעבודות שמבצעים הרכיבים בנפרד יש משמעות פיזיקלית מסוימת. הכוח $\mathbf{F} _y$ מניע את האלקטרון לאורך התיל ובכך יוצר זרם מושרה. העבודה שהוא מבצע שווה לכא”מ המושרה. הכוח $\mathbf{F} _x$ שואף לעצור את תנועת התיל ולכן בכדי שהתיל ינוע צריך להפעיל כוח בכיוון הנגדי באותו הגודל (בהזנחת כוח החיכוך). לפיכך, השקול הוקטורי של כל הרכיבים $\mathbf{F} _y$ הפועלים על כל האלקטרונים בתיל שווה לערכו המוחלט לגודל הכוח שיש להפעיל על התיל עצמו בכדי שהוא ימשיך לנוע במהירות קבועה.
אם כן, כאשר מוליך נע בתוך שדה מגנטי מתבצעות שלוש עבודות השוות בערכן המוחלט: עבודה $W _{\mathrm{ext}}$ של הכוח החיצוני שמופעל על המוליך ועוזר לו לנוע, עבודה $W_x$ של כל הרכיבים $F_x$ הפועלים על כל האלקטרונים במוליך והמתנגדים לתנועתו, והעבודה $W_y$ של כל הרכיבים $F_y$ הפועלים על האלקטרונים והגורמים ליצירת הזרם החשמלי המושרה. כמו כן, מתקיים:

\[W_{\mathrm{ext}}=-W_x=W_y\]

כלומר כל האנרגיה החיצונית המושקעת בהנעת המוליך עוברת לאלקטרונים וגורמת ליצירת הזרם המושרה.