כאשר אלומת אור פוגעת בגוף היא מוחזרת ממנו חלקית, חלקית עוברת דרכו וחלקית נבלעת בתוכו. ברוב המקרים האנרגיה של האור הפוגע הופכת לאנרגיה פנימית של הגוף וכתוצאה מכך הוא מתחמם. אבל לפעמים מתרחשות תופעות אחרות. החשובות ביותר הן האפקט הפוטואלקטרי, פוטולומינסנציה ותגובות פוטוכימיות. אך אנו נדון רק באחת מהן – באפקט הפוטואלקטרי.

בכדי להבין את מהות התופעה, נבצע את הניסוי הפשוט הבא. נחבר לוחית מאבץ טהור לאלקטרוסקופ ונאיר עליה באמצעות נורה הפולטת אור על-סגול (למשל נורת כספית-קוורץ), כמתואר באיור הבא.

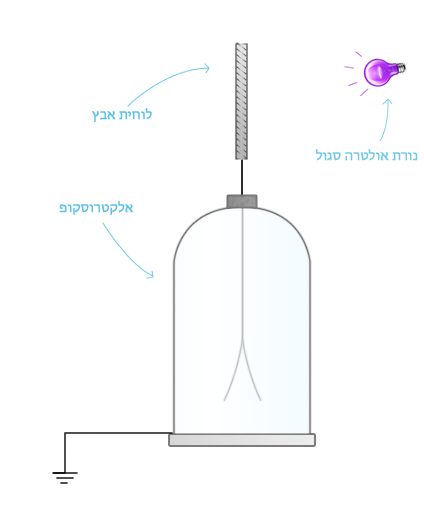
איור 1 – אפקט פוטואלקטרי – כתוצאה מקרינת האור המתכת מאבדת מטען שלילי (אלקטרונים)

אם האלקטרוסקופ היה מלכתחילה טעון שלילית, נגלה כי תחת השפעת הקרינה האולטרה סגולה תתרחש פריקה, כלומר המטען השלילי יפחת עם הזמן. הפריקה תתרחש מהר יותר אם נגדיל את שטף האור הפוגע ליחידת שטח. מסתבר גם שאם נשים זכוכית האטומה לאור אולטרה סגול לפני המקור, לא תתרחש פריקה. כמו כן, אם האלקטרוסקופ טעון חיובית, המטען שעליו יישמר ולא תתרחש פריקה, אף על פי שיפגע בו אור אולטרה סגול.

מניסוי זה ומניסויים אחרים רבים, ניתן להסיק את המסקנות הבאות:

1. מתכת מאבדת מטען שלילי כאשר מקרינים עליה אור.
2. מטען חיובי נשאר על פני מתכת גם אם מקרינים עליה אור.

במתכות, נושאי המטען השלילי הינם האלקטרונים. לפיכך אנו למדים כי האלקטרונים נעקרים מפני המתכת כאשר מקרינים עליה אור. תופעה זו נקראת האפקט הפוטואלקטרי. הפיזיקאי הרוסי אלכסנדר סטולטוב היה אחד הראשונים שהצליח להסביר כי בתהליך נעקרים אלקטרונים (מתוך ניסויים שערך בשנות 1888-1889).
מהניסוי אפשר להבין גם כי כאשר אלקטרון נעקר מפני גוף מתכתי שטעון שלילית, השדה החשמלי של הגוף גורם לו להתרחק ממנו. לעומת זאת, שדה של גוף הטעון חיובית מעכב את האלקטרון שנעקר, כלומר הוא שואף להחזירו למתכת. זאת אומרת שאם האנרגיה הקינטית של האלקטרון (ולכן גם מהירותו) לא מספיק גדולה, הוא לא יוכל לעזוב את המתכת בגלל השדה החשמלי גם אם נקרין עליה אור.
בכל מקרה, יכולת האור לעקור אלקטרונים מפני מתכות עלולה להיחשב כהוכחה ברורה של האופי הגלי של האור. אפשר לחשוב כי גל האור הפוגע במתכת “מטלטל” את האלקטרונים מה שגורם להם בסופו של דבר להשתחרר ממנה. אך מסתבר שזה לא כל כך פשוט כמו שזה נראה. אם זה באמת היה נכון, הרי שהיינו מצפים לכך שעם הגדלת משרעת גל האור מהירות האלקטרונים הנפלטים הייתה גדלה. דהיינו האנרגיה הקינטית שלהם צריכה להיות תלויה במשרעת. ניסויים שנערכו מראים כי לא כך הדבר.

נחזור לניסוי הראשון שלנו. כפי שהסקנו, האפקט הפוטואלקטרי מאופיין על ידי מספר האלקטרונים הנפלטים ליחידת זמן ועל ידי מהירותם. ככל שמספר האלקטרונים המשתחררים מפני המתכת ליחידת זמן גדול יותר, כך גם תהליך פירוק האלקטרוסקופ מתרחש מהר יותר; ככל שמהירות האלקטרונים גדולה יותר, כך גם השדה חייב להיות חזק יותר בכדי לעצור אותם.

על מנת למדוד מאפיינים אלו של האפקט הפוטואלקטרי (זרם ומהירות האלקטרונים) נבצע ניסוי אחר. ניקח שתי אלקטרודות ונחבר אותן להדקי סוללה כפי שמתואר באיור 2. האלקטרודות יימצאו במיכל אטום שהאוויר מתוכו נשאב על מנת למנוע התנגשויות של האלקטרונים עם מולקולות גז.

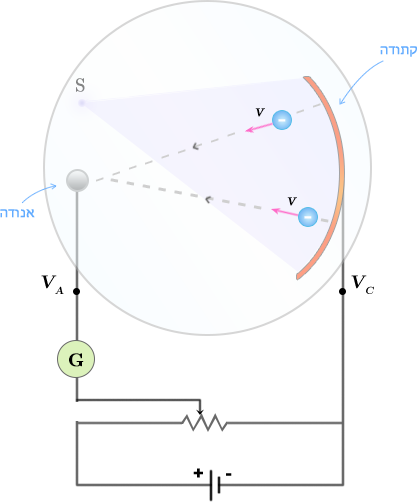
איור 2 – אלקטרודות הנמצאות במיכל ריק יוצרות קבל כדורי

מקור $S$ פולט קרינה אולטרה סגולה שפוגעת בקתודה ועוקרת אלקטרונים מפניה. המתח שנוצר בין האלקטרודות $V_{AC}$ ניתן לשינוי על ידי נגד משתנה. השדה שנוצר בגלל המתח בין האנודה לקתודה ($V_{AC} > 0$) מושך את האלקטרונים הנפלטים אל האנודה (זכור כי האלקטרונים נעים נגד קווי השדה) ולכן גם הגלוונומטר $G$ (מד זרם רגיש) יורה על זרם במעגל. הזרם שנוצר במעגל כתוצאה מהארת האלקטרודה נקרא זרם פוטואלקטרי. האלקטרונים הנפלטים נקראים פוטואלקטרונים.
ככל שנגדיל את המתח כך גם הזרם הפוטואלקטרי יגדל מפני שמספר רב יותר של אלקטרונים ישיג את האנודה. אם נגדיל בהדרגה את המתח, נגלה כי באיזשהו שלב השדה החשמלי יהיה כה חזק שכל האלקטרונים שיוצאים מהקתודה יגיעו לאנודה. אם כן, הערך המקסימלי של הזרם הפוטואלקטרי (שיסומן ב-$I_{\mathrm{sat}}$) נקבע על פי מספר האלקטרונים שנפלטים מהקתודה ליחידת זמן וקוראים לו גם זרם הרוויה. במילים אחרות, זרם הרוויה הינו זרם פוטואלקטרי שנוצר כאשר כל האלקטרונים הנעקרים מהקתודה מגיעים לאנודה:

\[I_{\mathrm{sat}}=en\]

כש-$n$ – מספר האלקטרונים הנפלטים מהקתודה ליחידת זמן.

אולם אם נהפוך את כיוון השדה החשמלי (למשל על ידי הפיכת הדקי הסוללה) כך שהשדה יהיה מכוון מהקתודה לאנודה ($V_{AC}<0$), השדה ישאף להחזיר את הפוטואלקטרונים לקתודה. אם נגדיל את המתח ניווכח כי עם הזמן השדה החשמלי יהיה מספיק חזק בכדי למנוע מכל האלקטרונים להיפלט מהקתודה. לפי גודל המתח המעכב הזה נוכל לגלות גם את המהירות המקסימלית של האלקטרונים הנפלטים.
נניח כי המהירות המקסימלית של האלקטרון הנפלט היא $v_{\mathrm{max}}$ (מסתו תסומן ב-$m$ ומטענו ב-$-e$). אזי האנרגיה הקינטית שלו שווה ל-$\frac{1}{2}mv_{\mathrm{max}}^2$. אלקטרון כזה יגיע לאנודה כאשר כל האנרגיה הקינטית שלו התבזבזה על עבודה נגד השדה החשמלי, לכן באנודה מהירותו תהיה שווה לאפס. אם נמצא את הערך המקסימלי של $V_{AC}=-V_0$ (או את הערך המינימלי של $V_{CA}=V_0$) עבורו אף אלקטרון לא יעבור לאנודה, נוכל בקלות למצוא את המהירות המקסימלית של האלקטרונים באמצעות משפט עבודה-אנרגיה:

\[\begin{align*} W=-e\left(V_{C}-V_{A}\right) & =-eV_{0}=\Delta E_{k}=0-E_{k,\mathrm{max}}\\ E_{k,\mathrm{max}} & =\frac{1}{2}mv_{\mathrm{max}}^{2}=eV_{0}\\ v_{\mathrm{max}} & =\sqrt{\frac{2eV_{0}}{m}} \end{align*}\]

הערך המינימלי של המתח המעכב $V_{CA}=V_0$ נקרא מתח עצירה.

חוקי האפקט הפוטואלקטרי

במהלך השנים באופן אמפירי גילו שלושה חוקים מרכזיים של אפקט פוטואלקטרי:

1. המהירות ההתחלתית המקסימלית של האלקטרונים הנפלטים מהמתכת תלויה בתדירות האור ואיננה תלויה בעוצמת האור.

2. לכל חומר קיימת תדירות סף $f_0$ כך שאור בעל תדירות נמוכה יותר לא יגרום לפליטת אלקטרונים ממנו, ללא תלות בעוצמת האור.

3. מספר האלקטרונים הנפלטים מהגוף ליחידת זמן (זרם הרוויה) נמצא ביחס ישר לעוצמת האור.

בנוסף לכך מסתבר כי הזרם הפוטואלקטרי נוצר מייד עם הקרנת האור, ללא השהיה, בתנאי שתדירות האור הפוגע מקיימת $f \geq f_0$.
אפשר להיווכח כי החוק הראשון והשני עומדים בסתירה למסקנות שאפשר להסיק בנוגע לאפקט הפוטואלקטרי מהתורה האלקטרומגנטית של האור.
הקשיים הללו נפתרו כאשר בשנת 1905 אלברט איינשטיין הציג גישה אחרת – התורה הקוונטית של האור.

הסבר קוונטי לחוקי האפקט הפוטואלקטרי

כידוע, אלקטרונים כל הזמן נעים בצורה כאוטית במתכות אך אינם בורחים החוצה. זה מעיד על כך שיש כוחות מסוימים המונעים מהם לצאת. על מנת להוציא את האלקטרון (מה שקורה באפקט הפוטואלקטרי) יש לבצע עבודה מסוימת, הנקראת עבודת יציאה, כנגד השדה החשמלי שמחזיק אותם על פני המתכת. אם כן, לגיטימי לשאול כיצד תלויים מספר האלקטרונים הנפלטים ומהירותם בחומר ממנו עשויה המתכת שעליה מקרינים אור? ובכן, מסתבר כי לכל חומר קיימת עבודת יציאה שונה, דהיינו לכל חומר אופיינית אנרגיה מינימלית מסוימת שצריך למסור לאלקטרון בכדי שהוא יוכל להתגבר על הכוחות שמחזיקים אותו.
נניח שמקרינים על מתכת כלשהי שעבודת היציאה שלה $A$ אור בעל תדירות $f$. נניח גם כי מהירות האלקטרונים הנעקרים היא $v$, כלומר יש להם אנרגיה קינטית $\frac{1}{2} mv^2$. אם כן, כל האנרגיה שנמסרה לאלקטרון היא $E=A+\frac{1}{2} mv^2$. מניסויים רבים מסתבר שהאנרגיה הכוללת $E$ שנמסרת לאלקטרון נמצאת ביחס ישר לתדירות האור, כלומר

\[E=A+\frac{1}{2} mv^2=h f\]

כאשר $h$ – גודל קבוע כלשהו. לנוסחה זו קוראים נוסחת איינשטיין לאפקט הפוטואלקטרי. הקבוע $h$ לא רק שלא תלוי בתדירות האור, אלא הוא גם זהה עבור כל החומרים! למעשה, מדובר בקבוע יסודי. קוראים לו בשם קבוע פלאנק, על שם הפיזיקאי המפורסם מאקס פלאנק. אפשר למדוד קבוע זה בניסויים שתוארו לעיל, שכן הגדלים $A$, $mv^2$ ו-$f$ ניתנים למדידה. מסתבר ש-$h$ שווה ל-$6.6 \cdot 10^{-34} \text{J} \cdot \text{s}$.
אם כן, נוכל לנסח את החוק הראשון של האפקט הפוטואלקטרי גם בצורה הבאה:

האנרגיה הכוללת שמוסר אור בעל תדירות $f$ לאלקטרון שווה ל-$hf$.

לחוק הזה יש חשיבות עצומה. לפיו הגברת עוצמת האור תגדיל את מספר האלקטרונים שיקבלו אנרגיה והחלשת עוצמת האור – תקטין את מספר האלקטרונים שיקבלו אנרגיה. אך כולם יקבלו את אותה מנת האנרגיה – $hf$. כמו כן, הוא גם מוכיח את אי-נכונותה של הקונספציה הגלית בכל הקשור לאפקט הפוטואלקטרי.
לאנרגיה של האור יש אופי אטומיסטי – אנרגיית אור לא יכולה “להתחלק”. היא תמיד מגיעה במנות מאוד מסוימות. למנות אנרגיה כאלה קוראים קוונטים של אור או פוטונים. באור מונוכרומטי בעל תדירות $f$ לכל הפוטונים אותה האנרגיה – $hf$. בליעת אור זה בעצם תהליך שבו הפוטונים הנבלעים מעבירים את כל האנרגיה שלהם לאטומים של החומר. זה אומר שתהליך בליעת האור איננו תהליך רציף.

משוואת איינשטיין מסבירה את כל חוקי האפקט הפוטואלקטרי. היא מוכיחה שהאנרגיה הקינטית המקסימלית של פוטואלקטרון תלויה בתדירות האור $f$ ובעבודת היציאה $A$, ואיננה תלויה בעוצמת האור (החוק הראשון של האפקט הפוטואלקטרי).
כמו כן, מאותה המשוואה נובע גם שהאפקט הפוטואלקטרי אפשרי אך ורק כאשר $hf \geq A$. זאת מפני שאנרגיית הפוטון הפוגע צריכה להספיק לפחות לעקירת אלקטרון, כלומר לביצוע עבודת יציאה, מבלי לתת לו אנרגיה קינטית. לפיכך נוכל לסמן ב-$f_0$ את התדירות הנמוכה ביותר שעבורה האפקט הפוטואלקטרי עוד יתקיים – תדירות הסף:

\[hf_0=A\] \[f_0=\frac{A}{h}\]

(החוק השני של האפקט הפוטואלקטרי)

ולבסוף, מושג הקוונטים של אור מאפשר לנו להבין גם את החוק השלישי של האפקט הפוטואלקטרי. עוצמת האור שהיא האנרגיה המועברת על ידי האור ליחידת זמן תלויה במספר הפוטונים המגיעים ליחידת זמן. ברור כי ככל שמספר הפוטונים רב יותר, כך גם מספר האלקטרונים שיקבלו את האנרגיה וייפלטו יהיה גדול יותר. בדרך מתמטית נוכל לרשום כי המספר הכולל $n$ של הפוטואלקטרונים העוזבים את המתכת ליחידת זמן צריך להיות פרופורציוני למספר הפוטונים $n^{\prime}$ הפוגעים במתכת באותו פרק הזמן ($n \propto n^{\prime}$). אם נסמן ב-$\Phi$ את שטף האור הפוגע במתכת ליחידת שטח, נוכל לרשום:

\[n^{\prime} \propto \frac{\Phi}{hf}\]

ומפני ש-$\Phi$ פרופורציוני לעוצמת האור, הוכחנו בכך שמספר הפוטואלקטרונים הנפלטים ליחידת זמן פרופורציוני גם הוא לעוצמת האור (החוק השלישי של האפקט הפוטואלקטרי).
כמובן שזה לא אומר שמספר האלקטרונים הנפלטים ליחידת זמן חייב להיות שווה למספר הפוטונים הפוגעים לאותה יחידת זמן. לא כל פוטון מוסר אנרגיה לאלקטרון בודד. ההפך, רוב האנרגיה תעבור לאטומים ותגרום לגוף להתחמם. מניסויים שנערכו מסתבר כי פחות מ-$1\%$ מכלל אנרגיית האור הפוגע עוברת לאלקטרונים.

כל מה שאמרנו לעיל לגבי האפקט הפוטואלקטרי נכון רק למקרה בו פוטון בודד נבלע על ידי אלקטרון בודד במתכת. במקרים בהם עוצמת האור היא מאוד גדולה, למשל במקרה של קרינת לייזר, בהחלט יכול לקרות מצב שבו אלקטרון אחד בולע שני פוטונים זהים. במקרה כזה, חוקי האפקט הפוטואלקטרי כבר לא יתקיימו. מדוע? ובכן, סך האנרגיה של שני פוטונים זהים היא $2hf$, כלומר הם יתנהגו כמו פוטון אחד בעל תדירות כפולה מזו של כל אחד מהם בנפרד – $2hf=h\left(2f\right)$. זאת אומרת שתדירות האור היא כאילו כפולה. במקרה של בליעה רב-פוטונית תדירות האור האפקטיבית תהיה $nf$ (כאשר $n$ – מספר שלם) ולכן החוק לתדירות הסף במקרה זה מופר.

יישומים של האפקט הפוטואלקטרי

• שלטי טלוויזיה – השלט שולח אור אינפרא-אדום והטלוויזיה קולטת את האות כתוצאה מהאפקט הפוטואלקטרי.
• צינור PMT – נועד להפוך אור חלש לאותות חשמליים מוגברים. הפוטונים פוגעים בפוטוקתודה העשויה מחומר מוליך למחצה והאלקטרונים הנפלטים מואצים על ידי אלקטרודות חיוביות לצינורות מיוחדים בהם הזרם שהם יוצרים מוגבר על ידי שיטות אלקטרוניות שונות. עליהם מבוססים מכשירים לראיית לילה.
• סינטילטור – מכשיר שימושי באסטרונומיה. הוא פולט אור כאשר פוגעת בו קרינה קוסמית והאור הזה מועבר לפוטוקולט שהופך אותו לאות חשמלי מוגבר.