
עקיפת פרנל
לתופעה של גל העוקף קצוות של מכשול בלתי שקוף קוראים עקיפה (או דיפרקציה). באופן כללי יותר עקיפה זהו פיזור של גלים על פני חלקים בלתי אחידים של הסביבה. התופעה הזאת אופיינית לגלים מכל הסוגים.
עקיפה בולטת במיוחד כאשר מימדי המחסום ואורך הגל פחות או יותר שווים. לדוגמה, לגלי קול יש אורך של כמטר אחד, ואת העקיפה שלהם אפשר להרגיש בקלות (ניתן לשמוע קול מעבר לפינה). אבל במקרה של אור שאורך הגל שלו הוא בערך כמה מיקרומטרים, קשה לראות עקיפה במצבים רגילים. במשך הרבה זמן אפילו חשבו שאור תמיד מתפשט בקו ישר.
ההסבר האיכותי לעקיפה ניתן על ידי עקרון הויגנס. את ההסבר הכמותי ניסח לראשונה המהנדס הצרפתי אוגוסטן פרנל. בשנת 1818 הוא הציג את העבודה שלו שקרא לה “תזכיר לגבי עקיפה של אור” לאקדמיה הצרפתית למדעים במסגרת תחרות שהם ערכו. שנה לאחר מכן התזכיר שלו קיבל פרס והודפס בספרי האקדמיה.
אחד מחברי הוועדה שבדקה את עבודתו של פרנל היה המדען המפורסם סימאון פואסון. בהתבסס על התאוריה של פרנל, פואסון ביצע חישובים עבור שני מקרים פרטיים של עקיפה על מחסומים שונים, אותם לא ניתח פרנל, וקיבל תוצאות פרדוקסליות. במקרה הראשון הוא קיבל שבמרכז של צל גאומטרי הנופל מכדור קטן שאליו מופנה אור צריך להיות כתם בהיר. במקרה השני הוא הגיע לכך שאחרי שהאור עובר דרך סדק עגול הנמצא במרכזה של תבנית עקיפה מתקבל כתם שחור. החישובים של פואסון הוצגו בתור הוכחה לכך שהתאוריה של פרנל כושלת. אולם ניסויים שבוצעו לאחר מכן הוכיחו שכל התוצאות המתקבלות מהתאוריה של פרנל נכונות לגמרי. העובדה הזאת שיחקה תפקיד חשוב מאוד בהבנה שלאור יש גם תכונות גליות.
נדבר כעת על עקיפה לעומק. לשם כך ננתח עקיפה של אור על פני סדק עגול בפרגוד בלתי שקוף. באיור 1 הקשת $ABC$ מייצגת את חזית הגל שפולט מקור אור נקודתי $S$ בעת שהוא משיג את המחסום.

איור 1
לפי עקרון הויגנס כל נקודה של החזית הינה מקור של גלים משניים וההתאבכות שלהם, לפי התאוריה של פרנל, מסבירה את תבנית העקיפה על מסך $Z$.
על מנת לחשב את תוצאת ההתאבכות של הגלים המשניים, למשל בנקודה $D$ במרכז המסך, נשתמש בשיטה שהציע פרנל. נחלק את חזית הגל לאזורים (אזורי פרנל) בצורה הבאה: הפרש המרחקים מכל נקודה בקצה האזור למרכז המסך צריך להיות שווה לחצי אורך גל האור:
\[AD-KD=KD-LD=LD-MD=MD-BD=\frac{\lambda}{2}\]זה מאפשר לנו להשתמש בתכונה הידועה: גלים בעלי הפרש דרכים השווה לחצי אורך הגל (הנמצאים באנטי-פאזה) מבטלים זה את זה. עבור כל נקודה של אזור אחד אפשר למצוא נקודה מתאימה באזור סמוך, שממנה גלים יגיעו אל הנקודה $D$ באנטי-פאזה. בנוסף השטחים של כל האזורים כמעט שווים. לפיכך, תרומות האזורים הסמוכים בנקודה $D$ (למשל של הראשון והשני, השני והשלישי וכו’) כמעט מבטלות זה את זה.
עכשיו אנחנו יכולים להבין באילו תנאים אפשר לראות את “הפרדוקס של פואסון”. אם לסדק מתאים מספר זוגי של אזורי פרנל, במרכז המסך יהיה כתם כהה. אחריו תיהיה טבעת בהירה, אחריה טבעת כהה וכדומה. בצורה כזאת אנו ניווכח כי על המסך תיהיה מערכת של טבעות כהות ובהירות לסירוגין, אבל הכתם במרכז יהיה כהה (איור 2).

איור 2 |
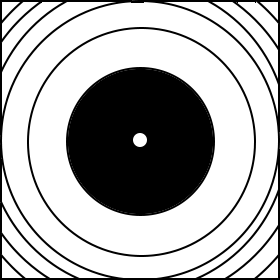
איור 3 |
אם מספר האזורים הוא אי-זוגי, התוצאה תיהיה הפוכה – במרכז יהיה כתם בהיר המוקף בטבעות כהות ובהירות לסירוגין. את תבנית העקיפה שנוצרת מכדור קטן המוצגת באיור 3 נסו להסביר בכוחות עצמכם.
תבנית העקיפה נעשית יותר מדוייקת כאשר מספר אזורי פרנל איננו גדול. למשל עבור אור נראה שאורך הגל שלו הוא $5 \cdot 10^{-7}~\text{m}$, עם מחסום בעל קוטר של $1~\text{mm}$, ומרחקים מסדר גודל של $1~\text{m}$ בין המחסום למקור אור והמסך מקבלים מספר קטן יחסית של אזורים על פני המחסום. במצב כזה רואים בבירור את הטבעות הכהות והבהירות. אם מגדילים את מימדי המחסום (או אם מקטינים את המרחקים) התבנית שנקבל תיהיה פחות ברורה.
כיום ניתן לצפות לא רק בעקיפה של אור אלא גם בעקיפה של קרינה קצרת גל כמו קרינת רנטגן. אורך הגל של קרינת רנטגן שווה לכמה עשרות אנגסטרמים (נזכיר כי $\overset{\lower.5em\circ}{\mathrm{A}} = 10^{-10}~\text{m}$). ליצור מחסומים מלאכותיים מסדר גודל כזה מאוד קשה. אך אם נשתמש בגביש שבו המרחקים הבינאטומיים הם בדיוק מסדר גודל זה, נקבל תבנית עקיפה הנקראת תבנית לאואה (על שם המדען הגרמני מקס פון לאואה שהציע לראשונה להשתמש בגביש על מנת לראות תבנית עקיפה של קרני רנטגן).
תבנית לאואה מורכבת מכתמים בעלי אינטנסיביות שונה הממוקמים סביב כתם מרכזי (איור 4 – תבנית לאואה של גביש נתרן). המראה של התבנית נקבע ע"י "אופן האריזה" של האטומים בגביש. ניסויים בעקיפה של קרני רנטגן לא רק שהוכיחו את הטבע הגלי של קרינת רנטגן אלא גם איפשרו להבין את המבנה הגאומטרי של גבישים שונים.
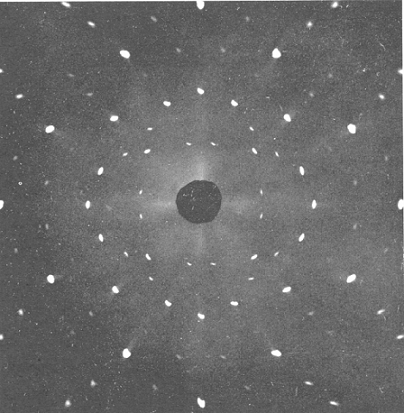
איור 4 (באדיבות אוניברסיטת קליפורניה בסן דייגו)