
סימטריה בבעיות בחשמל
הרבה בעיות בפיזיקה בכלל ובאלקטרומגנטיות בפרט עלולות להיראות קשות יתר על המידה ממבט ראשון. אך לעיתים ניתן לזהות תכונה אחת בבעיה אשר תאפשר לנו לפתור אותה כמעט בעל פה. התכונה המופלאה הזאת נקראת סימטריה ואנו נדון במאמר זה על תרומתה לפתרון בעיות מתחום החשמל.
רובנו שמענו על מושג הסימטריה ופגשנו אותו “בפעולה” בחיי היום יום, אך אם נשאל אנשים “מהי סימטריה?” בהרבה מקרים אנו לא נקבל הסבר מדוייק. סימטריה תמיד התקשרה ליופי, לאידיאליות ולהרמוניה בטבע, אך מהי בעצם סימטריה? סימטריה היא אי-השתנות (אינווריאנטיות) של מערכת תחת התמרות (טרנספורמציות) כלשהן. למשל, אם מדברים על סימטריה גאומטריות כמו סימטריית שיקוף, הרי שהכוונה היא לכך שהמערכת תיראה אותו הדבר אם נבצע שיקוף שלה לאורך ציר שיקוף מתאים.
מסתבר שמלבד היופי של הסימטריה היא גם מאוד שימושית בפתרון בעיות פיזיקליות שונות. אולם לא תמיד פשוט לזהות אותה. נראה כמה דוגמאות.
שש נקודות
נתונות שש נקודות כאשר כל נקודה מחוברת לנקודה אחרת באמצעות נגד בעל התנגדות $R$. מהי ההתנגדות השקולה בין שתי נקודות כלשהן?
מפני שלא נתון כיצד הנקודות ממוקמות אנו מייד מסיקים כי ארבעת הנקודות שלא נבחרו הן שוות ערך. למה הכוונה? הכוונה היא שקיימת סימטריית תמורה (permutation symmetry) ביחס לנקודות הללו, כלומר המערכת תיראה אותו הדבר אם נחליף מקומות בין נקודה כלשהי לבין נקודה אחרת מתוך ארבעת הנקודות שלא נבחרו. במילים אחרות – אין שום דבר שמבדיל בין הנקודות.
ניתן להציג את המערכת בצורת תמניון בכדי לראות ויזואלית את הסימטריה הקיימת:
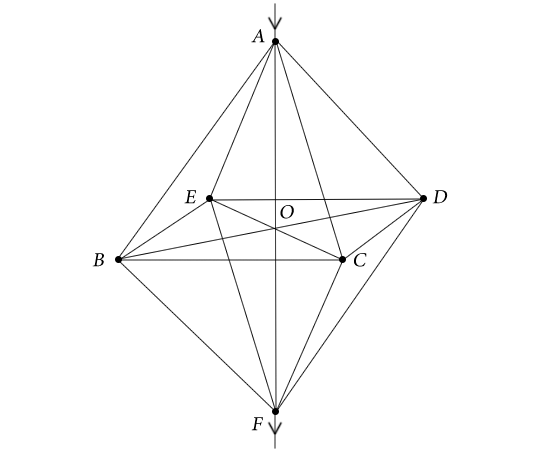
ב-$O$ הנגדים לא נחתכים (כמו כן, $O$ איננה נקודה בפני עצמה ונועדה לסימון בלבד); הנגדים מיוצגים ע"י קווים כתילים מוליכים
כפי שניתן לראות, קיימת סימטריה סיבובית ביחס לציר $AF$ – סיבוב של $90^{\circ}$ סביב ציר זה לא ישנה את המערכת.
אבל איך זה עוזר לנו? ובכן, מפני שהנקודות שוות ערך, הן בעלות אותו פוטנציאל חשמלי ולפיכך לא זורם בנגדים שמחברים ביניהן שום זרם. מפני שלא זורם זרם בנגדים הללו, אנו רשאים להסיר אותם מהמערכת (כי זה לא משנה האם יש נגד שלא זורם בו זרם או אין נגד בכלל). המערכת שלנו הופכת להיות פשוטה ביותר:
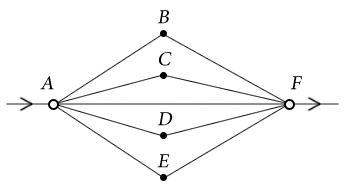
המערכת לאחר הסרת הנגדים שלא עובר בהם זרם
הנגדים המחברים את הנקודה השמאלית ואת הנקודה הימנית לנקודה העליונה מחוברים בטור ($R+R=2R$). כנ”ל לגבי שאר זוגות הנגדים. לאחר חיבור כל הנגדים המחוברים בטור, נקבל מערכת של נגדים המחוברים במקביל:
\[\frac{1}{R^{\prime}}=4 \cdot \frac{1}{2 R} + \frac{1}{R}\]לכן ההתנגדות השקולה $R^{\prime}$ תיהיה
\[R^{\prime}=\frac{R}{3}\]מעגל עם גשר
חשב את ההתנגדות השקולה בין הנקודות $A$ ו-$D$ במעגל החשמלי המתואר באיור.
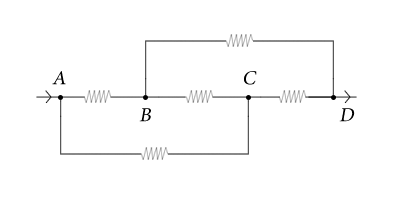
זוהי דוגמה טובה לבעיה שבה קשה יותר לראות את הסימטריה בצורה שבה המערכת נתונה לנו. לפיכך עלינו לסדר את המעגל בשלבים כך שיהיה נוח לראות את הסימטריה שקיימת בו:
1.
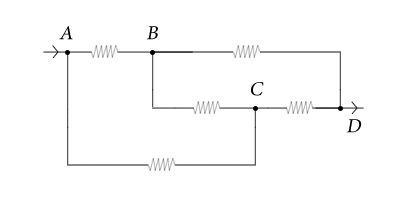
2.
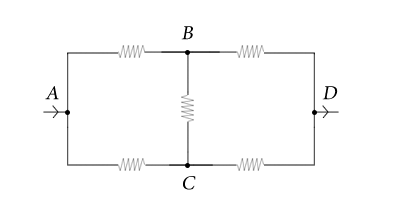
כעת ניתן לראות בבירור את הסימטריה השיקופית סביב ציר $AD$. אם נחליף מקומות בין הנקודה $B$ ל-$C$, המערכת תיראה אותו הדבר. זה אומר שהנקודות הללו שוות ערך ולפיכך הפוטנציאל החשמלי שלהם זהה. מכאן שלא זורם זרם בנגד שמחבר ביניהן. אפשר לראות זאת גם מחוקי קירכהוף – מפני שכל הנגדים הינם בעלי התנגדות זהה, הרי שבענף $ABD$ זורם אותו זרם כמו בענף $ACD$, לכן המתח בין נקודות $A$ ו-$B$ שווה למתח בין נקודות $A$ ו-$C$, מה שמוביל אותנו למסקנה שהנקודות $B$ ו-$C$ בעלות אותו פוטנציאל. כאמור, ניתן להסיר את הנגד אם לא זורם בו זרם, לפיכך אפשר להסיר את הנגד שמחבר בין $B$ ל-$C$.
נשארים לנו שני נגדים בענף $ABD$ המחוברים במקביל לשני הנגדים בענף $ACD$. כלומר ההנתגדות השקולה:
לכן:
\[R^{\prime}=R\]