
תנועה מעגלית קצובה
כאשר מסה נקודתית נעה במסלול מעגלי היא נעה בתאוצה, כי מהירותה כל הזמן משנה כיוון. בערכה המוחלט, המהירות יכולה להישאר קבועה, אולם כאשר אנו מדברים על מהירות, יש לזכור כי מדובר בווקטור שיש לו לא רק גודל, אלא גם כיוון.
ניקח את המקרה הפשוט של מסה נקודתית המבצעת תנועה מעגלית מבלי לשנות את גודל המהירות (כלומר $|\vec{\mathbf{v}}|=v=\text{const}$). תנועה כזאת נקראת תנועה מעגלית קצובה. נצייר וקטור מהירות בנקודת זמן שונות ונחברם לנקודה אחת (ניתן להזיז וקטורים כרצוננו כל עוד אנחנו לא משנים את גודלם או את כיוונם).
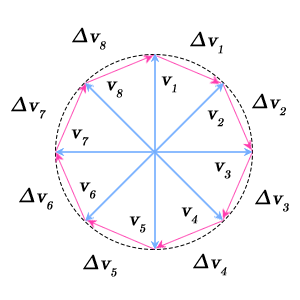
לפי כללי חיסור וקטורים ברור שניתן לייצג שינוי בווקטור המהירות (הפרש בין וקטורי מהירות עוקבים) על ידי בסיס של משולש שווה-שוקיים. נצייר את כל השינויים ($\Delta \mathbf{v}_i$) עבור סיבוב אחד. סכום כל השינויים עבור סיבוב שלם יהיה שווה לסכום צלעות המצולע המשוכלל שבציור. כמובן שהציור מתאר רק חלק מווקטורי המהירויות בתנועה מעגלית קצובה, והרי שהשינוי בכיוון וקטור המהירות מתרחש כל הזמן ללא הפסקה, לכן הציור רק נועד להמחשת הרעיון. כמו כן, ברור שהציור יהפוך להיות יותר מדויק ככל שנקטין את זוויות הראש של כל משולש או, לחלופין, ככל שניקח יותר ויותר וקטורי מהירות בפרקי זמן קטנים יותר. ככל שצלעות המצולע שלנו יהיו קטנות יותר, כך הוא יתקרב יותר למעגל בעל רדיוס $v$ (לא להתבלבל עם מסלול התנועה המעגלי). לכן הערך המדויק של סכום כל שינויי המהירות בערך מוחלט עבור סיבוב שלם יהיה ההיקף של המעגל – $2 \pi v$. ניתן לקבל את התאוצה של המסה הנקודתית על ידי חילוק של ההיקף הזה בזמן המחזור $T$ (הזמן שלוקח למסה להשלים סיבוב אחד):
\[a=\frac{2 \pi v}{T}\]מאידך, ניתן לבטא את זמן המחזור בתנועה במעגל ברדיוס $R$ באופן הבא – $T=\frac{2 \pi R}{v}$. כאשר נציב את הביטוי הזה עבור $T$ במשוואה הקודמת, נקבל את הביטוי הבא עבור גודל התאוצה של מסה נקודתית בתנועה מעגלית קצובה:
\[a=\frac{v^2}{R}\]במילים אחרות, כאשר רדיוס הסיבוב אינו משתנה התאוצה פרופורציונית לריבוע המהירות; עבור מהירות נתונה, התאוצה נמצאת ביחס הפוך לרדיוס.
מתוך האמור לעיל, ניתן גם להבין להיכן מכוונת התאוצה בכל נקודת זמן בתנועה מעגלית קצובה. ככל שזווית הראש בכל משולש בציור קטנה יותר, כך גם הזווית בין וקטור שינוי המהירות לבין וקטור המהירות עצמו קרובה יותר ל-$90^{\circ}$.
לכן, וקטור התאוצה בתנועה מעגלית קצובה מאונך לוקטור המהירות. ומכיוון שוקטור המהירות משיק למסלול המעגלי, הרי שוקטור התאוצה מתלכד עם הרדיוס ומכוון כלפי מרכז המעגל.
אם ננסה לסובב כדור באמצעות חבל, אנו נרגיש את הצורך להפעיל כוח עם השרירים על מנת לגרום לכדור לבצע תנועה מעגלית קבועה. למה יש צורך להפעיל כוח? הרי הגוף נע בתנועה קצובה? אז זהו, שלא. כאמור, הגוף נע במהירות קבועה בגודלה, אולם שינוי כיוון המהירות גורם לתנועה זו להיות תנועה מואצת. ובכדי לגרום לתאוצה, כידוע, יש להפעיל כוח.
לפי החוק השני של ניוטון, כיוון הכוח הוא ככיוון התאוצה. לפיכך, גוף הנע במסלול מעגלי במהירות הקבועה בגודלה צריך להרגיש כוח אשר יהיה מכוון כלפי מרכז המעגל, במקביל לרדיוס המעגל. כוח הפועל על גוף המבצע תנועה מעגלית קצובה נקרא הכוח הצנטריפטלי. גודל הכוח הצנטריפטלי שווה $m \frac{v^2}{R}$.
יש לציין כי הגוף שגורם לתנועה המעגלית (חבל, אדמה וכו’) הוא זה שמפעיל את הכוח הצנטריפטלי. כמו כן, חשוב להבין כי הכוח הצנטריפטלי איננו כוח בפני עצמו אלא שם לכל כוח באשר הוא הגורם לתנועה מעגלית; זה יכול להיות כוח מתיחות החוט או כוח חיכוך שמפעילה האדמה וכדומה.
כל הנאמר עד כה תקף גם במקרה של ירח וכדור הארץ. מה מחזיק את הירח בתנועה סביב כוכב הלכת שלנו? למה הירח לא מתרחק מכדה”א וממשיך לו לנוע במהירות קבועה ובקו ישר לפי החוק הראשון של ניוטון? כדור הארץ מחזיק את הירח במסלול המעגלי שלו באמצעות “חבל בלתי נראה” – כוח המשיכה. הכוח הזה שווה ל-$m \frac{v^2}{R}$ כאשר $v$ זאת המהירות של הירח, ו-$R$ זה המרחק מן המרכז של כדור הארץ ועד למרכז של הירח. היות ומסת כדה”א גדולה בהרבה ממסת הירח, ההשפעה של הירח על תנועת כדה”א זניחה.