
תנועה בליסטית
המטרה לזרוק עצם כמה שיותר רחוק העסיקה את האדם במשך אלפי שנים. אבן הנזרקת מהיד או מרוגטקה, חץ הנורה מקשת, קליע, פגז, טיל בליסטי – זאת רק רשימה קצרה של דוגמאות בנושא זה.
עצם שנזרק נע במסלול עקום הנקרא פרבולה. ניתן לצייר את המסלול הזה אם מסתכלים על התנועה של הגוף כסכום של שתי תנועות – תנועה אופקית ותנועה אנכית, אשר מתרחשות בעת ובעונה אחת וללא תלות של אחת בשנייה. תאוצת הנפילה החופשית מכוונת אנכית כלפי מטה, לכן העצם מתמיד במצבו בציר האופקי, כלומר נע במהירות קבועה בציר זה ובאותו הזמן מתקדם בציר האנכי בתאוצה קבועה. איך ניתן לחבר את שתי התנועות הללו?
נניח לשם פשטות כי המהירות ההתחלתית של קליע הינה אופקית (למשל במקרה בו קנה הנשק אופקי).
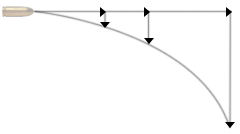
מכיוון ששתי התנועות אינן תלוייות זו בזו, אחרי $t$ שניות הגוף יזוז $v_0 t$ ימינה ו-$\frac{gt^2}{2}$ למטה. לפי שתי המשוואות הללו ניתן לצייר את הציור המוצג לעיל על ידי הצבה של נקודות זמן ומיפוי של הערכים במערכת צירים מתאימה. אנו נראה כי כאשר נחבר את הנקודות נקבל מסלול עקום – פרבולי. בכדי לקבל את המסלול המדוייק יש לצייר הרבה נקודות קרובות זו לזו.
במקרה של מהירות התחלתית אשר איננה מקבילה לאף ציר, יש לפרק את וקטור המהירות לרכיבים. הרכיב האופקי מייצג את המהירות ההתחלתית של הגוף בכיוון אופקי בעוד שהרכיב האנכי מייצג את המהירות ההתחלתית האנכית. נניח כי הקליע נורה בזווית עם האופק כלפי מעלה. מכאן שאחרי $t$ שניות הקליע יזוז $\mathbf{v}_x t$ ימינה ו-$h=\mathbf{v}_y t-\frac{gt^2}{2}$ למעלה. לפי הנוסחה האחרונה, ניתן למצוא את שיעורי הנקודות על הציר האנכי ברגעים המעניינים אותנו ובכך למפות את המסלול בציר זה. בהתחלה $h$ יגדל אך אחרי כמה זמן הוא יתחיל לקטון.
אם אנו נחזיק את הקנה של הנשק אופקית, הקליע יגיע מאוד מהר לקרקע; במצב שבו הקנה אנכי, הקליע פשוט יתרומם מעל הנקודה שממנו נורה ויפול בהדרגה אל אותה הנקודה. לכן, בכדי לירות כמה שיותר רחוק, צריך למקם את הקנה באיזושהי זווית לאופק. אך השאלה היא באיזו?
נלך בדרך שתיארנו קודם – נפרק את הוקטור של המהירות ההתחלתית לשני רכיבים: בציר האנכי המהירות ההתחלתית שווה ל-${v}_y$, בציר האופקי היא שווה ל-${v}_x$. מהנוסחה $v = v_0+ gt$ נובע שהזמן שלוקח לקליע להגיע לנקודה המקסימלית בציר האנכי הוא $v_y/g$. אותו הזמן בדיוק ייקח גם עד שהקליע יפול בחזרה. לכן הזמן הכולל שהקליע היה באוויר הינו $2 v_y / g$. מכיוון שבכיוון האופקי המהירות קבועה, הרי שטווח הזריקה שווה
\[d=\frac{2 v_y v_x}{g}\]קיבלנו נוסחה, המראה כי המרחק המקסימלי של הזריקה פרופורציוני למכפלת רכיבי המהירויות. באיזו זווית של הקנה המכפלה הזאת תיהיה הכי גדולה? על מנת לענות על השאלה הזאת, יש להיזכר בחוקים גאומטריים של חיבור וקטורים. המהירויות $v_x$ ו-$v_y$ יוצרות מלבן של מהירויות. האלכסון של מלבן זה, זאת המהירות המקורית $v$. מכפלת הרכיבים נותנת את השטח של המלבן הזה.
השאלה שלנו שקולה לשאלה הבאה: עבור אלכסון נתון של מלבן, אילו צלעות יש לקחת על מנת לקבל את השטח המקסימלי? בגאומטריה ניתן להוכיח כי ריבוע עונה על התנאי. לכן המרחק המקסימלי שהקליע יעבור יהיה כאשר הרכיבים יהיו שווים (כי צלעות של ריבוע שוות). אלכסון של ריבוע יוצר זווית של $45^{\circ}$ עם כל צלע, ובפרט עם צלע אופקית (במקרה שלנו – הרכיב האופקי של המהירות) לכן זאת הזווית שבה צריך להחזיק את הקנה על מנת שהקליע יעוף כמה שיותר רחוק. ניתן למצוא בעזרת חוקים גאומטריים ותכונות של ריבוע גם את היחס שבין גדלי הרכיבים לבין גודל המהירות הכוללת, וגם למצוא את היחס שבין הגובה שאליו יעלה הקליע לבין המרחק האופקי שיעבור עד לפגיעה בקרקע.
יש לציין כי כל האמור לעיל לא ייתן תוצאות מדוייקות בחיים האמיתיים. הנוסחאות הללו תקפות רק במקרים בהם אין התנגדות אוויר, מפני שהגורם הזה משנה באופן דרמטי את התמונה הכללית.