
חוק שימור אנרגיה במכניקה ושגיאות נפוצות
את חוק שימור האנרגיה המכנית ניתן לקבל מתוך חוקי ניוטון, בהנחה שהכוחות הפועלים במערכת תלויים במרחק שבין גופים או בין חלקים המרכיבים את הגופים במערכת (כוחות משיכה ואלסטיות).
המושגים העיקריים בהם משתמשים במקרה זה הם עבודה, אנרגיה קינטית, אנרגיה פוטנציאלית ואנרגיה כוללת. כל המושגים הללו, פרט לאנרגיה פוטנציאלית, לא קשים במיוחד לעיכול. ולמרות זאת, בלימודי מכניקה הרבה פעמים נוטים להסיק מסקנות שגויות כאשר לומדים את חוק שימור האנרגיה. הסיבה לכך מצד אחד היא, שכנראה, הלומדים לא מבינים עד הסוף את המשמעות העמוקה של מושגי היסוד הללו, ומצד שני (וזאת הנקודה החשובה), הרבה פעמים על מנת להקל על ההבנה נוטים להסתכל על דוגמאות פשוטות וספציפיות מאוד, ואחר כך מתוכם ללא הרבה מחשבה מסיקים מסקנות כלליות יותר, אשר לא תמיד נכונות. אנו נדון במאמר זה בשגיאות הנפוצות שעושים בלימודי חוק שימור האנרגיה במכניקה.
עבודה
נזכיר את מושג העבודה. עבודה של כוח $\mathbf{F}$ בהעתק כה מינימלי $\Delta \mathbf{s}$ של גוף עליו הוא פועל, כך שניתן להתייחס אל הכוח כאל קבוע בגודלו ובכיוונו, שווה (איור 1):
\[A=|\mathbf{F}| |\Delta \mathbf{s}| \cos{\alpha} \tag{1}\]כאשר $\alpha$ – זווית בין וקטור $\mathbf{F}$ לבין וקטור $\Delta \mathbf{s}$. במילים אחרות, עבודה מוגדרת בתור מכפלה סקלרית של וקטורים $\mathbf{F}$ ו-$\Delta \mathbf{s}$, כלומר
\[A=\mathbf{F} \cdot \Delta \mathbf{s}\]אם הגוף נע בקו ישר והכוח $\mathbf{F}$ קבוע, הנוסחה (1) תקפה עבור כל העתק, לא משנה עד כמה הוא גדול.
לפעמים נוטים לומר שההעתק נגרם בגלל הכוח. זה לא נכון. זה כלל לא משנה, מה גורם להעתק. אם במהלך תנועה של גוף פועל עליו כוח כלשהו, העבודה שמבצע כוח זה שווה לרכיב הכוח בכיוון ההעתק, כפול ההעתק עצמו.

איור 1
מכאן נובע, שעבודה איננה מתבצעת כאשר גוף עליו מופעל הכוח לא נע ביחס למערכת הייחוס הנתונה. למשל, כאשר גוף מחליק עם חיכוך על פני משטח כלשהו (איור 2), כוח החיכוך $F_1$ הפועל על הגוף מבצע עבודה, בעוד שכוח החיכוך $F_2$ הפועל על המשטח המקובע, לא מבצע שום עבודה.
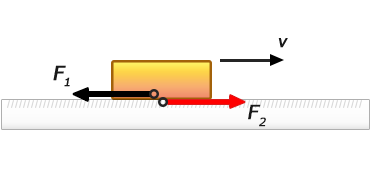
איור 2 – כוח החיכוך $\mathbf{F}_1$ הפועל על הגוף מבצע עבודה, בעוד שכוח החיכוך $\mathbf{F}_2$ הפועל על המשטח המקובע, אינו מבצע עבודה
כמובן שגודל העבודה הנעשית על ידי כוח כלשהו, תלוי במערכת הייחוס שאנו בוחרים. וזאת מפני שגוף הנח במערכת ייחוס אחת, ינוע במערכת ייחוס אחרת הנעה ביחס למערכת הייחוס הראשונה. למשל, אם אדם עומד ברכבת ומחזיק קפיץ במצב מתוח המחובר אל דופן הרכבת, הרי שבמערכת הייחוס הצמודה לרכבת, היד שלו לא תבצע שום עבודה, מפני שהחלק החופשי של הקפיץ לא זז. אולם מנקודת מבט של צופה במערכת ייחוס הצמודה אל כדור הארץ, כן תתבצע עבודה, מפני שכל המערכת נמצאת בתנועה. עוד דוגמה. הרבה פעמים אומרים כי עבודת כוח חיכוך ההחלקה תמיד שלילית. אך למעשה, היא יכולה להיות גם חיובית. זה פשוט תלוי בבחירת מערכת ייחוס.
אנרגיה קינטית
אחד המושגים הקלים ביותר להבנה הינו המושג של אנרגיה קינטית. תוך שימוש בהגדרה של עבודה ובאמצעות החוק השני של ניוטון, ניתן להראות כי בכל המקרים העבודה הנעשית על ידי כוח כלשהו $\mathbf{F}$ שווה לשינוי באנרגיה הקינטית של הגוף $K=\frac{mv^2}{2}$:
\[A=\mathbf{F} \cdot \Delta \mathbf{s}=\Delta K \tag{2}\]יותר מזה, מקור הכוח וסוג הכוח כאן לא משנים בכלל. זה יכול להיות כוח משיכה, כוח אלסטיות או כוח החיכוך.
אנרגיה קינטית של גוף מסוים מוגדרת באמצעות מסתו ומהירותו, והיא לא תלוייה בכך האם הגוף נמצא באינטראקציה עם גופים אחרים או לא. כמו כן, מפני שאנרגיה איננה גודל וקטורי, אין משמעות לכיוון תנועתו של הגוף. גודל אנרגיה קינטית תלוי, כמו במקרה של עבודה, במערכת הייחוס שאנו בוחרים.
האנרגיה הקינטית של מערכת של גופים שווה לסכום האנרגיות הקינטיות של גופי המערכת.
אנרגיה פוטנציאלית – אנרגיית אינטראקציה בין גופים
הרבה פעמים שוכחים להדגיש שאנרגיה פוטנציאלית במכניקה הינה אנרגיית אינטראקציה של לפחות שני גופים. מושג האנרגיה הפוטנציאלית קשור למערכת של גופים ולא לגוף אחד. אם במערכת ישנם מספר גופים, האנרגיה הפוטנציאלית הכוללת של המערכת שווה לסכום האנרגיות הפוטנציאליות של כל זוגות הגופים אשר נמצאים באינטראקציה זה עם האחר.
בדרך כלל, כאשר מפתחים את הנוסחה המקשרת בין שינוי אנרגיה פוטנציאלית של מערכת לבין עבודה של כוחות במערכת זו, מתייחסים לאחד הגופים כאל נַייָח. למשל, כאשר דנים בבעיית נפילה של גוף אל כדור הארץ תחת השפעת כוח הכובד, ניתן להזניח את ההעתק של כדור הארץ. לכן עבודה של כוחות אינטראקציה בין כדור הארץ לבין הגוף הופכת לעבודה של כוח אחד בלבד, הפועל על הגוף. עוד דוגמה. קפיץ מתוח או מכווץ אשר מפעיל כוח על גוף מסוים, בדרך כלל מחובר מצידו האחד אל גוף אחר, למשל קיר, כך שהקצה הזה לא מסוגל לזוז (למעשה הוא מחובר אל כדור הארץ), ובכך הקפיץ עצמו נשאר מקובע. במקרה כזה, רק הכוח האלסטי הפועל על הגוף מבצע עבודה.
זאת הסיבה לכך שנוהגים להסתכל על אנרגיה פוטנציאלית כעל אנרגיה של גוף בודד. זה לא נכון ועלול להוביל לבלבול מיותר.
בפועל, נכון לומר את הדבר הבא: השינוי באנרגיה פוטנציאלית של שני גופים, המפעילים זה על זה כוחות אשר תלויים רק במרחק שבין הגופים, שווה למינוס העבודה של כוחות אלו:
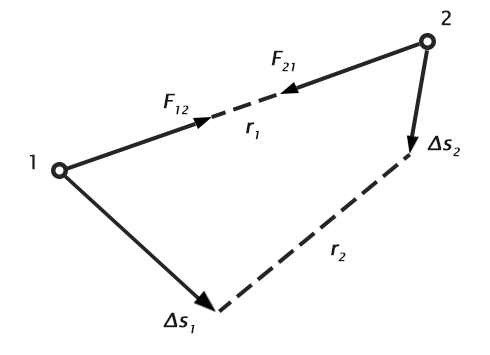
איור 3 – השינוי באנרגיה פוטנציאלית של הגופים 1 ו-2 נקבעת על ידי עבודת הכוחות $\mathbf{F} _{12}$ ו-$\mathbf{F} _{21}$ בהעתקים $\Delta \mathbf{s}_1$ ו-$\Delta \mathbf{s}_2$
כאשר $\mathbf{F} _{12}$ – כוח שמפעיל גוף 2 על גוף 1 ו-$\mathbf{F} _{21}$ – כוח שמפעיל גוף 1 על גוף 2.
כוחות האינטראקציה בין הגופים, אשר תלויים אך ורק במרחק בין הגופים, הינם כוחות משמרים. וזאת מפני שעבודה של כוחות משמרים תלוייה אך ורק במיקום ההתחלתי והסופי של הגופים, ואיננה תלוייה במסלול שלהם. כמובן שזאת לא בעיה לחשב את שינוי האנרגיה הפוטנציאלית אם אנו יודעים את הביטוי המקשר בין כוח לבין המרחק.
רמת האפס של אנרגיה פוטנציאלית
ממשוואה (3) נובע כי עבודה של כוחות מבטאת לא את האנרגיה הפוטנציאלית עצמה אלא את השינוי בה. עבור כוח כובד בקרבת כדור הארץ, ניתן לרשום:
\[\Delta U_g=mgh_2-mgh_1 \tag{4}\]כאשר $h_1$ ו-$h_2$ – גבהים מעל פני כדור הארץ שבהם נמצא הגוף במצב ההתחלתי והסופי.
שינוי האנרגיה הפוטנציאלית של קפיץ מכווץ או מתוח:
\[\Delta U_e=\frac{k (\Delta l_2)^2}{2}-\frac{k (\Delta l_1)^2}{2} \tag{5}\]כאשר $k$ – קבוע הקפיץ (מקדם הקשיחות) ו-$\Delta l_1$ ו-$\Delta l_2$ – העיוות ההתחלתי והסופי של הקפיץ (שינוי באורך הקפיץ).
מפני שעבודה מבטאת את השינוי באנרגיה פוטנציאלית ולא את האנרגיה הפוטנציאלית עצמה, רק השינוי באנרגיה פוטנציאלית הינו בעל משמעות פיזיקלית. לכן, ניתן לבחור בצורה שרירותית כזה מצב של מערכת אשר בו האנרגיה הפוטנציאלית שווה לאפס. המצב הזה הינו רמת האפס של אנרגיה פוטנציאלית. בחירת רמת האפס מתבצעת במצבים שונים באופן שונה, כאשר נוחות זה הגורם הקובע. ניתן לראות דמיון בין בחירת רמת האפס של אנרגיה פוטנציאלית לבין בחירת ראשית של מערכת צירים. אנו יכולים להזיז את הצירים כרצוננו וזה לא ישפיע על מרחק שבין שתי נקודות קבועות.
בדרך כלל, בוחרים את רמת האפס של אנרגיה פוטנציאלית כך שה-$U$ יהיה מינימלי. במקרה כזה האנרגיה הפוטנציאלית תיהיה חיובית.
במקרה של קפיץ, האנרגיה הפוטנציאלית הינה מינימלית כאשר הוא איננו מְעוּוָת. בדוגמה של אבן, האנרגיה הפוטנציאלית תיהיה מינימלית על פני כדור הארץ. לכן במקרה הראשון:
\[U_e=\frac{k(\Delta l)^2}{2} \tag{6}\]ובמקרה השני
\[U_g=mgh \tag{7}\]אך לביטויים הללו ניתן להוסיף באופן שרירותי כל קבוע שנרצה, וזה לא ישנה שום דבר בחישובים שלנו. הרי רק להפרש בין אנרגיות פוטנציאליות יש משמעות פיזיקלית. לכן, ניתן בהחלט לרשום:
\[U_e=\frac{k(\Delta l)^2}{2}+C,~~U_g=mgh+C \tag{8}\]אם במקרה השני נניח כי $C=-mgh_0$, זה אומר שרמת האפס של אנרגיה פוטנציאלית נבחרה בגובה $h_0$ מעל פני כדור הארץ.
לפעמים, לא ניתן לבחור את רמת האפס של $U$ כך שהאנרגיה המינימלית תיהיה אפס. למשל, האנרגיה הפוטנציאלית הכובדית של שתי מסות נקודותיות היא
\[U=-G \frac{m_1 m_2}{r}+C \tag{9}\]כאשר $G$ – קבוע הכבידה העולמי ו-$r$ – המרחק בין המסות.
כאשר $r$ שואף לאפס, החלק הראשון בביטוי שואף לאינסוף. לכן האנרגיה המינימלית במקרה זה, תיהיה כאשר נניח כי $C=\infty $. אך זה מסובך ולא פרקטי להשתמש בביטוי אשר כולל בתוכו אינסוף. לכן במקרה זה, יותר נוח להניח כי $C=0$ וכתוצאה מכך לקבוע כי רמת האפס של אנרגיה פוטנציאלית תיהיה כאשר המרחק בין הגופים יהיה אינסופי ($r=\infty $). במקרה זה, ברמת האפס של האנרגיה הפוטנציאלית האנרגיה תיהיה דווקא המקסימלית ולא המינימלית. וזאת מפני שעבור כל ערך סופי של $r$ האנרגיה הפוטנציאלית תיהיה שלילית.
אי-תלות של שינוי אנרגיה פוטנציאלית במערכת ייחוס
נדגיש שוב, כי מושג האנרגיה הפוטנציאלית הינו בעל משמעות רק עבור אותן מערכות, שבהן כוחות האינטראקציה הינם כוחות משמרים, כלומר תלויים במרחק שבין גופים או רכיבי גופים בלבד. לכן גם ה-$U$ תלוי במרחק: בגובה של האבן מעל פני כדור הארץ, באורך הקפיץ, במרחק שבין מסות או מטענים נקודתיים. אנרגיה פוטנציאלית איננה תלוייה באופן ישיר במיקום של גופים (הקוֹאוֹרדִינָטָות שלהם במערכת צירים מסויימת). מכאן נובעת עובדה חשובה מאוד, אותה לא תמיד מזכירים. מפני שהמרחק בין שתי נקודות קבועות בכל מערכות ייחוס, לא משנה האם הן נעות או נייחות, הוא אותו המרחק, השינוי באנרגיה פוטנציאלית לא תלוי במערכת הייחוס הנבחרת.
איך זה ייתכן? הרי $\Delta U = -A$, ועבודה כן תלוייה במערכת ייחוס שאנו בוחרים! העניין הוא, שכאשר עוברים ממערכת ייחוס אחת לשנייה, ערכי שתי העבודות משתנים, אולם הסכום שלהם נשאר קבוע. נראה זאת בדוגמה הבאה. נניח כי במערכת ייחוס כלשהי, בזמן $t$ נעשית עבודה
\[A_1=\mathbf{F} _{12} \cdot \Delta \mathbf{s} _1 + \mathbf{F} _{21} \cdot \Delta \mathbf{s} _2\]מכאן שבמערכת השנייה, אשר נעה ביחס אליה, העבודה שווה ל-
\[A_2=\mathbf{F} _{12} \cdot \left(\Delta \mathbf{s} _1 +\Delta \mathbf{s} _0 \right) + \mathbf{F} _{21} \cdot \left(\Delta \mathbf{s} _2 + \Delta \mathbf{s} _0\right)\]כאשר $\Delta \mathbf{s} _0$ – ההעתק היחסי שבין שתי המערכות בזמן $t$. מחוק שלישי של ניוטון, אנו יודעים כי $\mathbf{F} _{12} = - \mathbf{F} _{21}$; מכאן נובע $\mathbf{F} _{12} \cdot \Delta \mathbf{s} _0 = - \left (\mathbf{F} _{21} \cdot \Delta \mathbf{s} _0 \right)$. לכן:
\[A_1=A_2\]
כעת, על מנת לחדד את הבנתכם, נסו לפתור את השאלה הבאה:
כדור בעל מסה $m$ משוחרר מגובה $h$ מעל הקרקע במערכת ייחוס $S$ הצמודה אל כדור הארץ. במערכת זו ברגע השחרור לכדור יש אנרגיה פוטנציאלית כובדית $mgh$ אשר מומרת לאנרגיה קינטית $\frac{mv^2}{2}$, כלומר $mgh=\frac{mv^2}{2}$. כעת נעבור למערכת ייחוס $S^{\prime}$ אשר נעה בכיוון נפילת הכדור במהירות $v=\sqrt{2gh}$. במערכת זו, המהירות ההתחלתית של הכדור היא $v=\sqrt{2gh}$ והמהירות הסופית (כהרף עין לפני ההתנגשות בכדה”א) היא אפס. לפיכך, האנרגיה התחלתית היא $E_i=\frac{mv^2}{2}+mgh=2mgh$ בעוד שהאנרגיה הסופית היא $E_f=0$. לאן נעלמה האנרגיה?