
דואליות גל-חלקיק של האור
האם אור זה תופעה של גל אלקטרומגנטי הנפלט על ידי מקור אור, או שהמקור פולט שטף של פוטונים הנעים במרחב במהירות האור בריק $c$?
על פניו נראה כי שתי נקודות המבט על תכונות האור – הגלית (האלקטרומגנטית) והקוונטית (החלקיקית) – נוגדות זו את זו. למשל, החלקיקים הנעים (הפוטונים) נמצאים באזורים מסוימים במרחב, בעוד שאל גל מתפשט יש להתייחס כאל “נמרח” במרחב ולא ניתן לדבר על הימצאות של גל באזור מסוים במרחב. הצורך לייחס לאור מצד אחד, תכונות גליות, ומצד אחר, תכונות קוונטיות, עלול להוביל למחשבה שאנחנו עוד לא סגורים על ההבנה שלנו בנוגע לטבעו של האור. אפשר אפילו לחשוב שניתן להסביר את כל התופעות הקשורות לאור על בסיס נקודת מבט אחת – גלית או חלקיקית.
עם התפתחות האופטיקה, הגיעה ההבנה שתכונות הרציפות של גל אור אשר מאוד אופייניות לשדה אלקטרומגנטי אינן נוגדות את התכונות הדיסקרטיות (אי-רציפות), אשר אופייניות לפוטונים. אור הינו בעל תכונות גליות וחלקיקיות בו זמנית.
את הדואליות של האור ניתן לראות בנוסחאות הבאות המתארות תכונות של פוטונים:
אפשר לראות שהתכונות החלקיקיות של הפוטון – האנרגיה $\varepsilon _{\gamma}$ והתנע $p _{\gamma}$ – קשורות לתכונה הגלית של האור – התדירות שלו $\nu$.
אלברט איינשטיין היה הראשון שהגיע למסקנת הדואליות גל-חלקיק של האור כאשר חקר תנודות אנרגיה ביחידת נפח אחת של קרינת גוף שחור ותנודות של לחץ האור (1909). מכיוון שלחץ האור פרופורציוני לעוצמתו, התנודות של הגדלים האלה צריכות להיות מבוטאות בנוסחאות זהות. איינשטיין השתמש בחוקים של קרינת גוף שחור, בכלים שעמדו לרשותו בפיזיקה סטטיסטית והגיע לנוסחאות הללו. הסתבר שהן מכילות סכום של שני איברים:
האיבר הראשון הוא “האיבר הקוונטי” שתואם לתפישה של האור כזרימה של פוטונים דיסקרטיים. האיבר השני הוא “האיבר הגלי” שמתאר תנודות בגל האלקטרומגנטי המתפשט. הנקודה החשובה ביותר כאן היא שרק הסכום של שניהים נותן את התנודות של אנרגיה ושל לחץ האור. בתדרים נמוכים יחסית, לאיבר הגלי יש יותר משקל והוא משחק את התפקיד היותר חשוב, בעוד שבתדרים גבוהים – האיבר הקוונטי הוא בעל המשקל הרב יותר.
לתופעות הדואליות של האור יש חוקיות חשובה ביותר. לקרינה ארוכת גל (למשל לאור אינפרא אדום) התופעות הקוונטיות פחות משמעותיות מאשר התופעות הגליות. אפשר להסביר בקלות תופעות אופטיות כמו התאבכות, עקיפה וקיטוב באמצעות הכלים שעומדים לרשותנו באופטיקה גלית. אבל ככל “שנתקדם” בסקאלה של גלים אלקטרומגנטיים, מגלים ארוכים לגלים קצרים, אנו ניווכח כי התופעות הגליות של האור ייחלשו בעוד שהתופעות הקוונטיות יתחזקו. רואים זאת בבירור בחוק של הגבול האדום באפקט הפוטואלקטרי (התדר הנמוך ביותר או הגל הארוך ביותר, שעבורם עוד מתקיים האפקט הזה). גילוי העקיפה של קרינת רנטגן קצרת הגל, היה אפשרי רק בגלל השימוש במבנה הגבישי של גופים מוצקים בתור סריג עקיפה. אחרת פשוט אי אפשר היה לראות את התכונות הגליות של קרינת רנטגן.
התכונות הגליות והקוונטיות של האור קשורות זו לזו. נראה קשר זה בניסוי של אלומת אור העוברת דרך סדק. נניח כי דרך הסדק $AB$, במקביל לציר $y$ עוברת אלומה של קרינה מונוכרומטית. כידוע, על המסך $CD$ שנמצא מאחורי הסדק, תופיע תבנית עקיפה. עוצמת ההארה $E$ בנקודה כלשהי על המסך פרופורציונית לעוצמת האור באותה הנקודה. כמובן ש-$E$ משתנה מנקודה לנקודה. באיור הבא מצד ימין אפשר לראות את התפלגות עוצמת האור לאורך המסך:
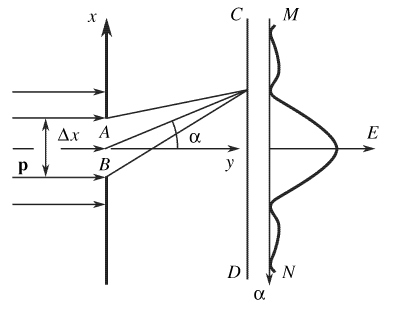
ניזכר כי עוצמת האור פרופורציונית לריבוע האמפליטודה (משרעת) $A$ של גל האור. מכאן שעוצמת ההארה $E$ בכל נקודה על המסך פרופורציונית לריבוע האמפליטודה של גל האור בנקודה זו, כלומר $E \sim A^2$. מנקודת ראות קוונטית, היווצרות תבנית עקיפה על המסך מעידה על כך שכאשר האור עובר דרך הסדק מתרחשת חלוקה מחדש של הפוטונים במרחב. כתוצאה מכך בנקודות שונות של המסך פוגעת כמות שונה של פוטונים. עוצמת ההארה $E$ בנקודה נתונה תהיה גדולה יותר ככל שסך האנרגיה של כל הפוטונים הפוגעים בנקודה זו ליחידת זמן תהיה רבה יותר. האנרגיה הזאת תהיה פרופורציונית ל-$n_0$ הפוטונים שאיתם היא הגיעה. לפיכך, $E \sim n_0$.
נניח כי שטף האור העובר בסדק הוא כה חלש שאפשר להתייחס אליו כאל שטף שמורכב מכמות קטנה של פוטונים. בגבול, אפשר להתייחס לשטף כאל שטף שמורכב מפוטונים הנעים בזה אחר זה. במקרה זה היינו מצפים לתבנית עקיפה אחרת, אך לא כך הדבר. מניסויים מסתבר שאם מחלישים את השטף של האור, את עוצמתו, תבנית העקיפה איננה משתנה. היחס שבין אזורים חשוכים לבין אזורים בהירים על המסך, אשר אופייני לעקיפה עבור מכשול נתון, נשאר גם כאשר השטף של האור נחלש.
במציאות לא ניתן ליצור שטף שיהיה מורכב מפוטונים הנעים בזה אחר זה. בכדי ליצור ניסוי המקביל לניסוי התאורטי הזה, צריך לדמיין כי אנו חוזרים על הניסוי של פגיעת הפוטון בנקודה כלשהי על המסך הרבה פעמים. אם נצפה זמן רב בניסוי, התוצאה של “ירי הפוטונים על המכשול” תהיה זהה לתוצאה שהייתה מתקבלת אילו היה עובר שטף המורכב ממספר רב של פוטונים.
נשווה כעת את התוצאות שקיבלנו עבור עוצמת ההארה. מהם נובע כי $A^2 \sim n_0$. כלומר:
ריבוע האמפליטודה של גל אור בנקודה כלשהי במרחב פרופורציוני למספר הפוטונים העוברים בנקודה זו
במילים אחרות:
ריבוע האמפליטודה של גל אור בנקודה נתונה במרחב הינו מידת ההסתברות של פגיעת פוטונים בנקודה זו
אנו רואים כי התכונות הגליות והחלקיקיות של האור לא רק שלא נוגדות זו את זו, אלא גם משלימות זו את זו. התכונות הקוונטיות של האור נובעות מהעובדה שהאנרגיה והתנע של הקרינה מרוכזות בחלקיקים – פוטונים. ההסתברות להימצאות הפוטונים בנקודות שונות במרחב נקבעת על ידי התכונות הגליות של האור – האמפליטודה של גל האור.
התכונות ההסתברותיות של הפוטון באות לידי ביטוי בעובדה שאי אפשר לומר בוודאות באיזו נקודה בדיוק הוא יפגע אחרי שיעבור בסדק. ניתן לדבר רק על ההסתברות של כל פוטון לפגוע בנקודה כזאת או אחרת של המסך.